Otras herramientas
Problemas de aplicación
El uso de las Tecnologías de la Información y la Comunicación han cambiado el modo de vida de los seres en el planeta. La tecnología es un instrumento mediante el cual es posible dar respuestas y soluciones a muchos problemas prácticos de la vida cotidiana. Las necesidades son distintas y dependen, muchas veces, no solo del lugar geográfico, sino también del sistema de creencias y valores de una sociedad.
Así como el científico usa la tecnología para buscar respuestas a los problemas o el artista la utiliza para producir obras, el docente, debe aprovecharla para despertar en sus estudiantes la capacidad de síntesis y análisis que les permita interpretar su propia realidad, como un ser social activo con el propósito de tener una mejor calidad de vida para todos.
Para todo problema humano hay siempre una solución fácil, clara, plausible y equivocada.
Henry-Louis Mencken (1880-1956)
Problema

Don José desea colocar tres lámparas en su vivero, de manera tal que una de las lámparas quede en el camino principal. ¿Cuál es la menor cantidad de cable que ocupa don José?
Solución
Don José tiene que reflejar el punto $C$ sobre la recta $l$ (el camino) y obtener su punto simétrico $C'$. El $\overline{CC'}$ es perpendicular al camino y lo interseca en el punto $A$, de tal manera que $d(AC)=d(AC')$, luego $d(AB)+d(AC)$ equivale a la menor cantidad de cable que se ocupa.
Problema

En el vivero “El amigo de la tierra” se va a llevar a cabo una exposición de orquídeas. Ana María ha sido invitada a participar, pero los organizadores le dicen que debe colocar sus 20 orquídeas en forma parabólica, todas a una misma distancia de un punto fijo dado. Ayude a Ana María a colocar las orquídeas.
Solución
Ayude a Ana María a trazar la parábola, para ello siga los siguientes pasos:
- Trace un recta $l$ y sobre ella marque un punto $O$ y otro punto exterior $F$.
- Trace una perpendicular a la recta que pase por $O$.
- Trace la mediatriz del $\overline{FO}$, denomine, con $P_{0}$, al punto de intersección de la mediatriz con la perpendicular.
- Marque un punto $A$ sobre la recta, a la derecha de $O$ y trace una perpendicular que pase por $A$.
- Trace la mediatriz del $\overline{AF}$ y denomine, con $P_{1}$, al punto de intersección de la mediatriz con la perpendicular
- Repita los pasos 4 y 5, varias veces.
- Trace rectas paralelas a la recta $l$, que pasen por los puntos $P_{1}, \; P_{2}, \; \cdots$.
- Determine los puntos simétricos $P'_{1}, \; P'_{2}, \; \cdots$ de $P_{1}, \; P_{2}, \; \cdots$. Considere la perpendicular a la recta $l$, que pasa por $O$, como el eje de simetría.
- Sobre los puntos $P_{1}, \; P_{2}, \; \cdots$ y $P'_{1}, \; P'_{2}, \; \cdots$, Ana María debe colocar las orquídeas.
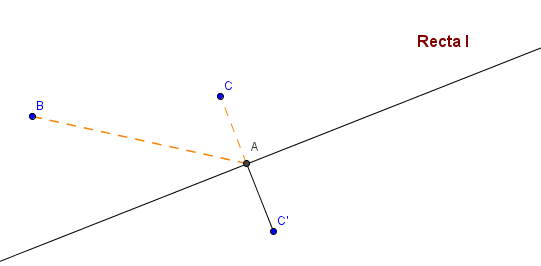 Fig. 114b Reflexión sobre una recta
Fig. 114b Reflexión sobre una recta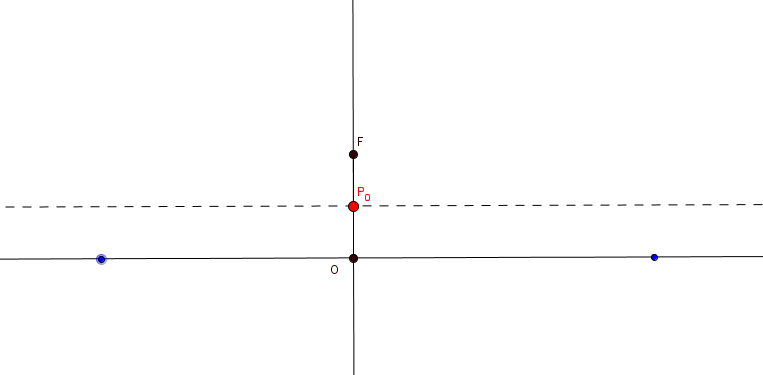 Fig. 116 Perpendicular a la recta
Fig. 116 Perpendicular a la recta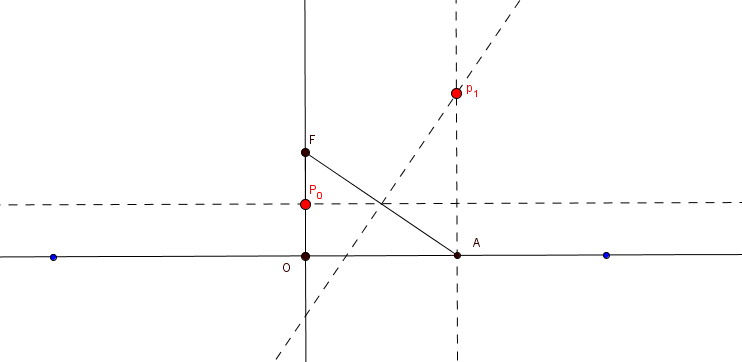 Fig. 117 Mediatriz del $\overline{AF}$
Fig. 117 Mediatriz del $\overline{AF}$ 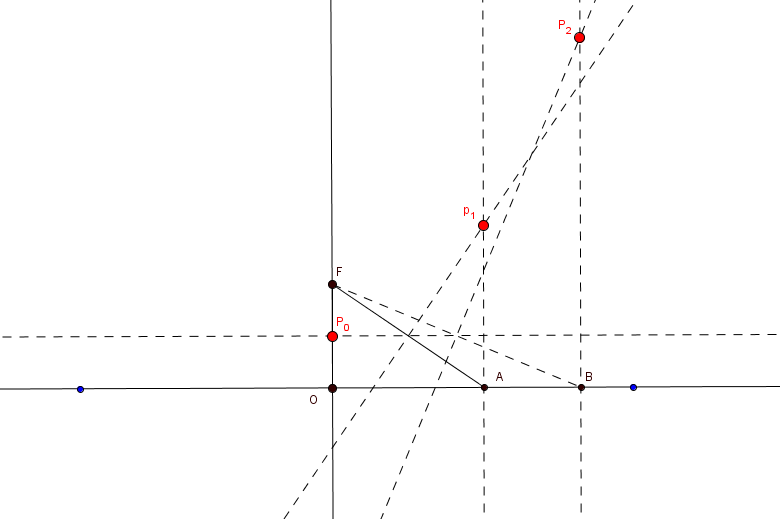 Fig. 118 Establecimiento de otros puntos $P$
Fig. 118 Establecimiento de otros puntos $P$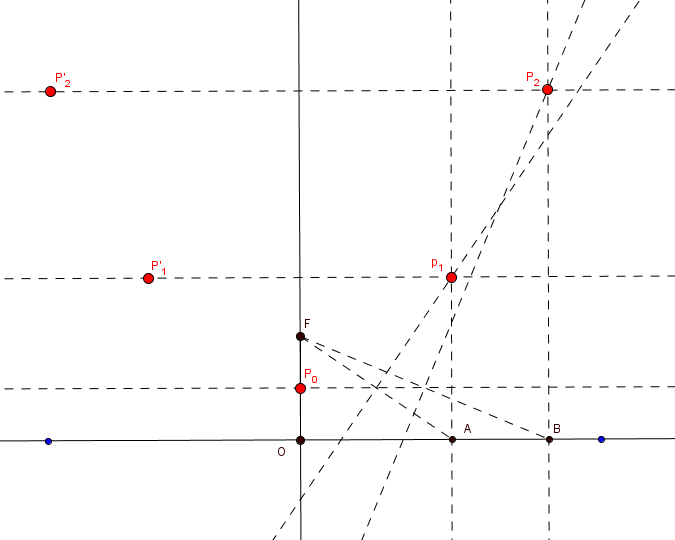 Fig. 119 Establecimiento de los puntos $P'$
Fig. 119 Establecimiento de los puntos $P'$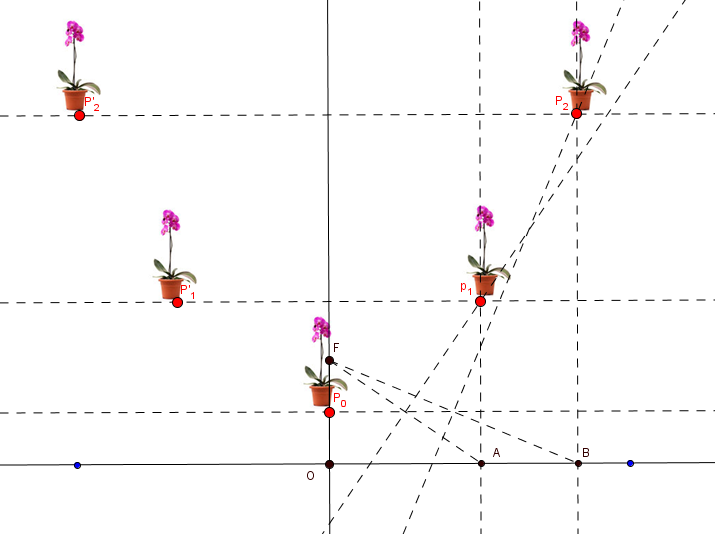 Fig. 120 Colocación de las orquídeas
Fig. 120 Colocación de las orquídeas