Otras herramientas
Construcciones
En este apartado se presentan algunas construcciones geométricas, utilizando el software libre Geogebra, el portasegmentos, la regla y el compás. Siga las recomendaciones que se le dan en los laboratorios anteriores.
Para realizar las construcciones con algún software se aconseja que siga las siguientes recomendaciones:
- Explore el programa para familiarizarse con la herramienta.
- Verifique si es compatible con el sistema operativo de su equipo.
- Consulte todos los tutoriales que se le ofrecen para su utilización.
- Si tiene problemas con el uso de la herramienta, consulte con un especialista en matemática.
Ahora, tome sus hojas de papel, la regla, el compás, el portasegmentos y su computadora y haga las construcciones que se muestran en este multimedia. ¡Anímese!
Procedimiento
- Trace dos circunferencias concéntricas de centro $O$ y radios iguales a los semiejes mayor y menor.
- Marque un punto $D$, en la circunferencia mayor.
- Trace la recta $\overleftrightarrow{OD}$. Denomine, con $F$, al punto de intersección de la recta con la circunferencia menor.
- Determine, los otros puntos de intersección de la recta, con las dos circunferencias.
- Trace rectas paralelas a los ejes, que pasen por los puntos de intersección $D$ y $F$, respectivamente.
- Denomine, con $G$, al punto de intersección de las rectas paralelas y active el trazo.
- Mueva el punto $D$, a través de la circunferencia mayor y compruebe que se dibuja la elipse.
Propiedad
La elipse es el lugar geométrico de los puntos del plano, cuya suma de las distancias a dos puntos fijos, llamados focos, es una cantidad constante.
Procedimiento
- Digite, en la ventana de entrada de Geogebra, $y=x-1$, $y=x+5$.
- Con la herramienta polígono, dibuje el $\triangle ABC$.
- Seleccione el $\triangle ABC$ y, con la herramienta Simetría Axial-objeto reflejar punto, marque la recta $y=x-1$.
- Seleccione el $\triangle A'B'C'$ y, con la herramienta Simetría Axial-objeto reflejar punto, marque la recta $y=x+5$.
- La distancia del $\triangle ABC$ al $\triangle A''B''C''$, es el doble de la distancia entre las rectas paralelas.
Propiedad
La reflexión de un objeto geométrico (preimagen), a través de dos rectas paralelas, es equivalente a una traslación de dicho objeto una distancia igual al doble, de la distancia entre las rectas paralelas.
Procedimiento
Existen muchos tipos de tubería y accesorios que se adaptan a las necesidades de cada industria, dentro de estos se encuentran los codos para tuberías. Construir este tipo de piezas es muy sencillo, si se cuenta con una regla y un compás.
- En un plano cartesiano, haga centro en el origen y trace el radio mayor y el radio menor del codo.
- Divida el cuadrante en el número de partes que considere conveniente. En este caso se divide en cuatro partes; primero, trace primero la bisectriz del ángulo de $90^{\circ}$ y, luego, la bisectriz del ángulo de $45^{\circ}$.
- Divida el diámetro en el número de partes que considere conveniente. En este caso se divide en $n=4$ partes. Haga centro en el origen y trace los arcos con radio, cuyos extremos son el origen y el punto de división.
- Denomine, con $A$ y $B$, los puntos donde dos bisectrices consecutivas intersecan al radio mayor.
- Trace la mediatriz del $\overline{AB}$.
- Denomine, con los puntos $C$, $D$, $E$, $F$, $G$, $H$, $I$, $J$, las intersecciones de las dos bisectrices consecutivas con los arcos trazados.
- Denomine, con los puntos $O_{1}$, $O_{2}$, $O_{3}$, $O_{4}$ y $O_{5}$, la intersección de la mediatriz del $\overline{AB}$ con los arcos trazados.
- Trace un segmento, cuya longitud sea el perímetro de una de las bases del codo, $P=2\cdot \pi \cdot r$, con $r$ el radio del círculo y divida dicho segmento, en el doble del número de partes en que dividió el diámetro, en este caso, $n=8$. Traslade con el compás las distancias de los segmentos $\overline{AB}$, $\overline{CD}$, $\overline{EF}$, $\overline{GH}$, $ \overline{IJ}$.
- Con una regla flexible, una los puntos para obtener la “plantilla” del codo.
- Construya cuatro plantillas y forme el codo.
Procedimiento
- Marque un segmento $\overline{AB}$ y un punto $C$ , tal que $A−C−B$, este segmento pertenece a la recta directriz.
- Marque un punto $F$, que corresponde al foco.
- Trace una perpendicular al $\overline{AB}$, que pase por el punto $C$.
- Trace la mediatriz del segmento $\overline{FC}$.
- Denomine, con $P$, al punto de intersección de la mediatriz con la perpendicular.
- Active el rastro del punto $P$ y mueva el punto $C$, a lo largo de $\overline{AB}$ para formar la parábola.
Propiedad
Se conoce con el nombre de parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y, una recta, llamada directriz.
Procedimiento
- Trace una recta $l$ , que contenga a los focos $F$ y $F'$.
- Trace la mediatriz de $\overline{FF'}$, etiquete, con $C$, al punto de intersección entre la mediatriz y el segmento.
- A partir de $C$, trace los vértices $A$ y $A'$, tal que $d(CA')=d(CA)=a$.
- Denomine, con $B$, un punto de la mediatriz y con $B'$ su simétrico, tal que $d(CB)=b$, con $b<a$ o $b>a$.
- Trace el rectángulo de largo $2a$ y ancho $2b$.
- Trace las diagonales del rectángulo, que serán las asíntotas de la hipérbola.
- Sobre la recta $l$, marque puntos $P_{1}, \; P_{2}, \; P_{3}, \; \cdots P_{n}$, a la derecha de $F$ y $P'_{1}, \; P'_{2}, \; P'_{3}, \; \cdots P'_{n}$, a la izquierda de $F'$.
- Con centro en los focos y radios $AP_{1}, \; A'P_{1}, \; \cdots AP_{n}, \; A'P_{n}$, trace los dos arcos, la intersección es un punto de la hipérbola.
- Repita el procedimiento, para los otros puntos.
Propiedad
El lugar geométrico de los puntos del plano, tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
Procedimiento
- Trace una recta $l$ y marque los puntos $F$, $A$ y $O$.
- Con la herramienta Rotación, rote los puntos $F$ y $A$ alrededor del punto $O$, con un ángulo de rotación de $180^{\circ}$.
- Marque un punto $P$ sobre la recta y defina los segmentos $\overline{PA}$ y $\overline{PA'}$.
- Con la herramienta Círculo[centro-radio], trace la circunferencia con centro en $F$ y radio $PA$.
- Con la herramienta Círculo[centro-radio], trace la circunferencia con centro en $F'$ y radio $PA'$.
- Etiquete, con $P_{1}$ y $P_{2}$, los puntos de intersección de las dos circunferencias. Estos puntos pertenecen a la hipérbola.
- Repita el procedimiento anterior, para los puntos que están a la izquierda de $F'$.
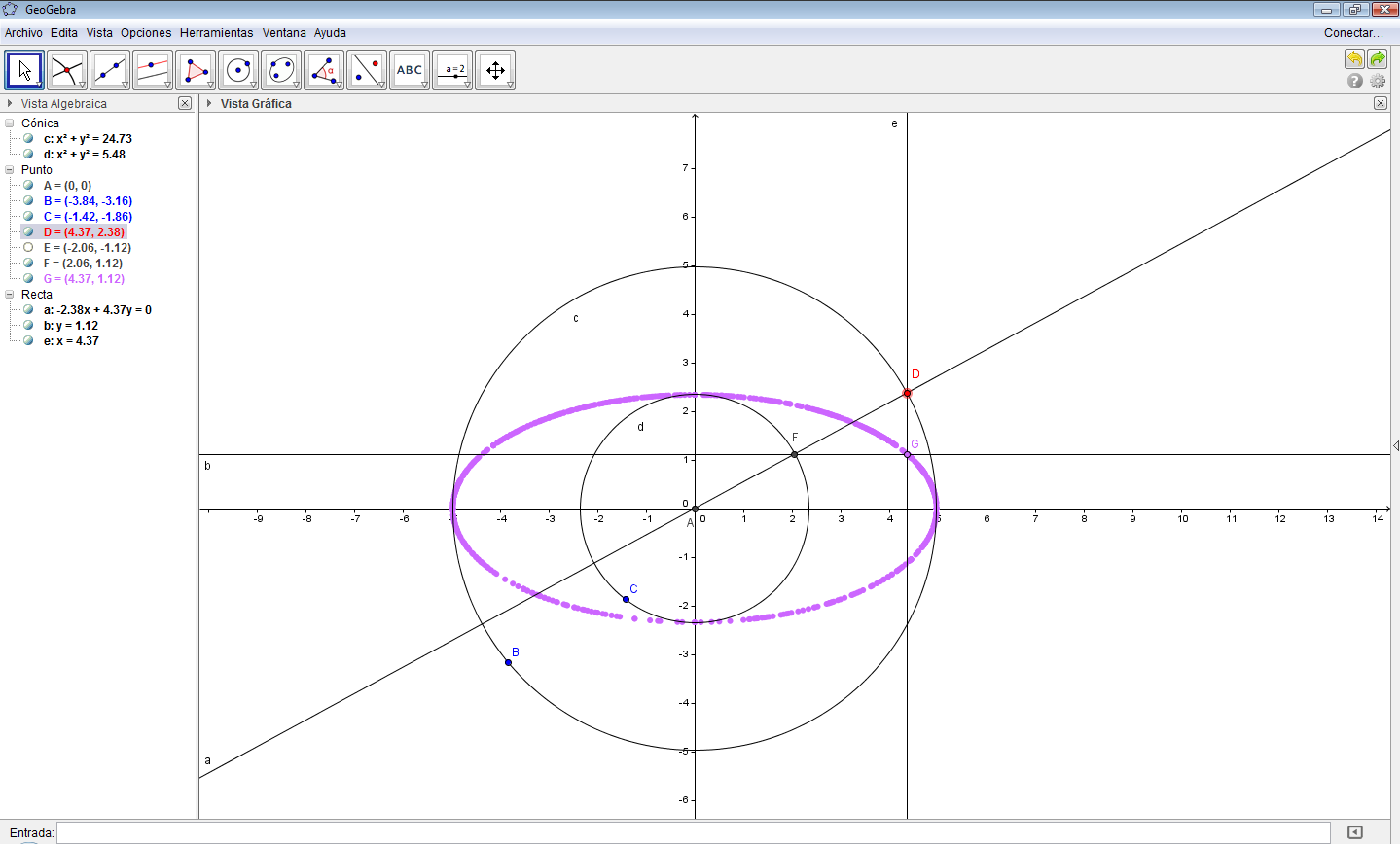 Fig. 95 Elipse en Geogebra
Fig. 95 Elipse en Geogebra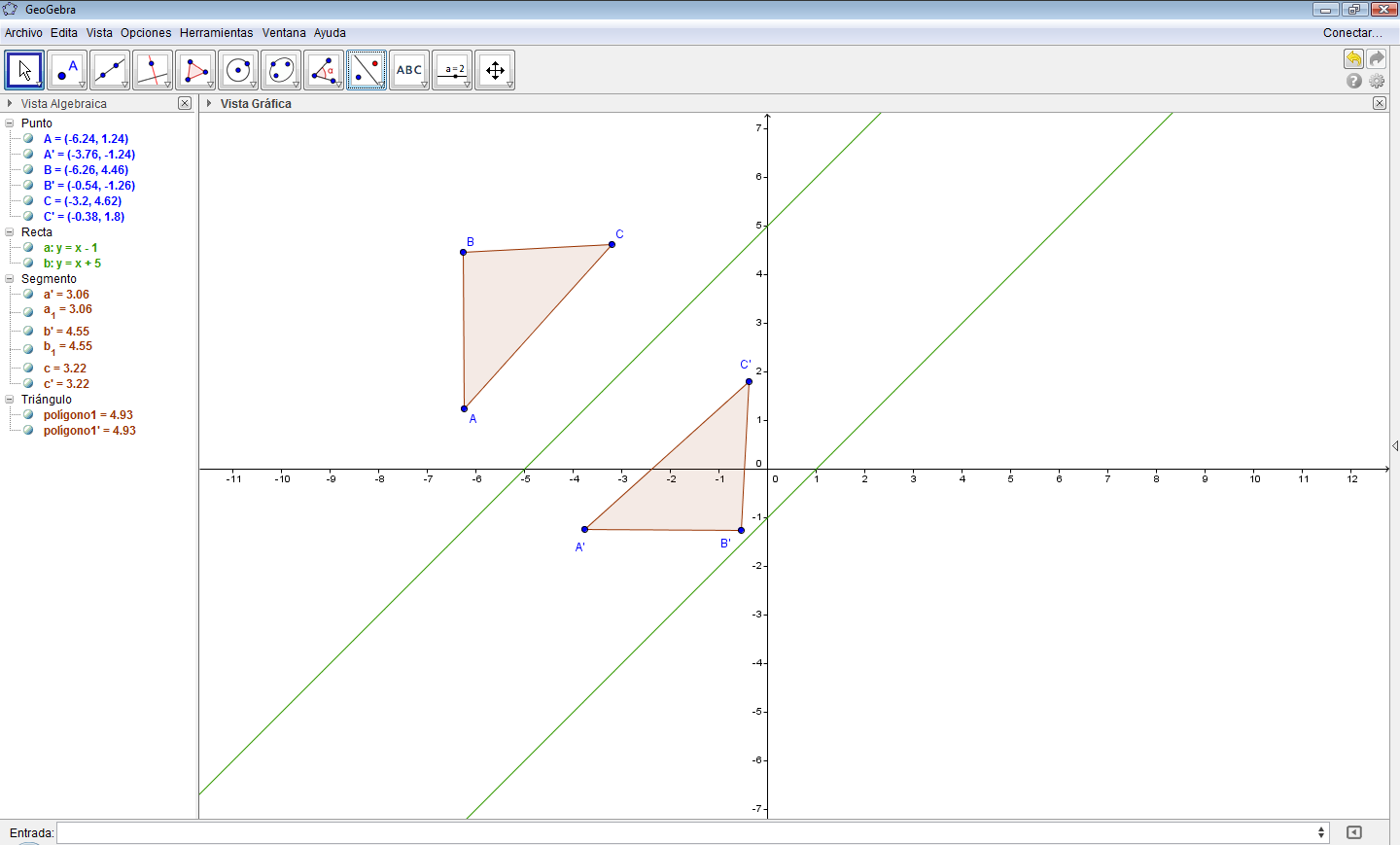 Fig. 96 Reflexión del triángulo a través de la primera recta
Fig. 96 Reflexión del triángulo a través de la primera recta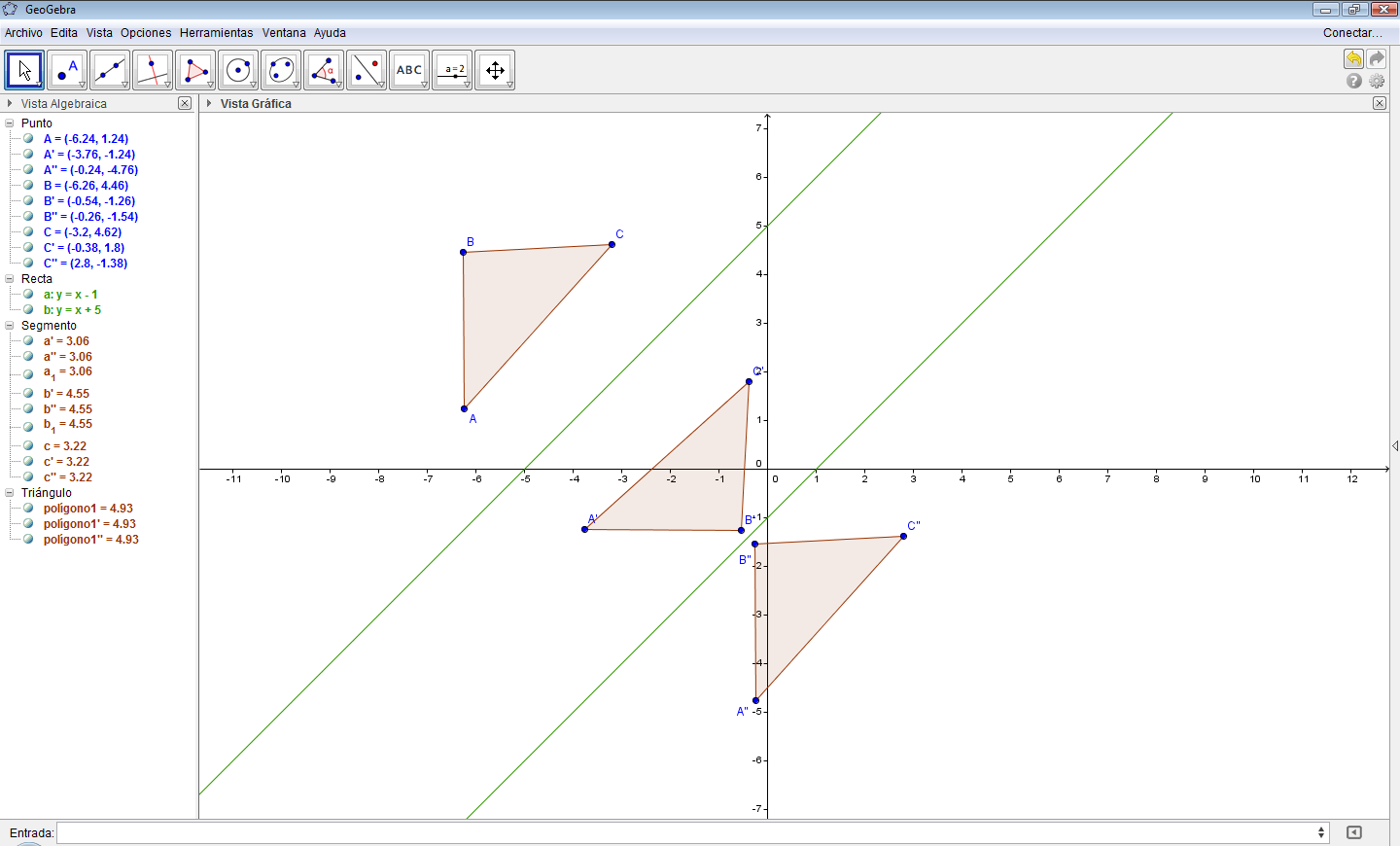 Fig. 97 Reflexión del triángulo a través de la segunda recta
Fig. 97 Reflexión del triángulo a través de la segunda recta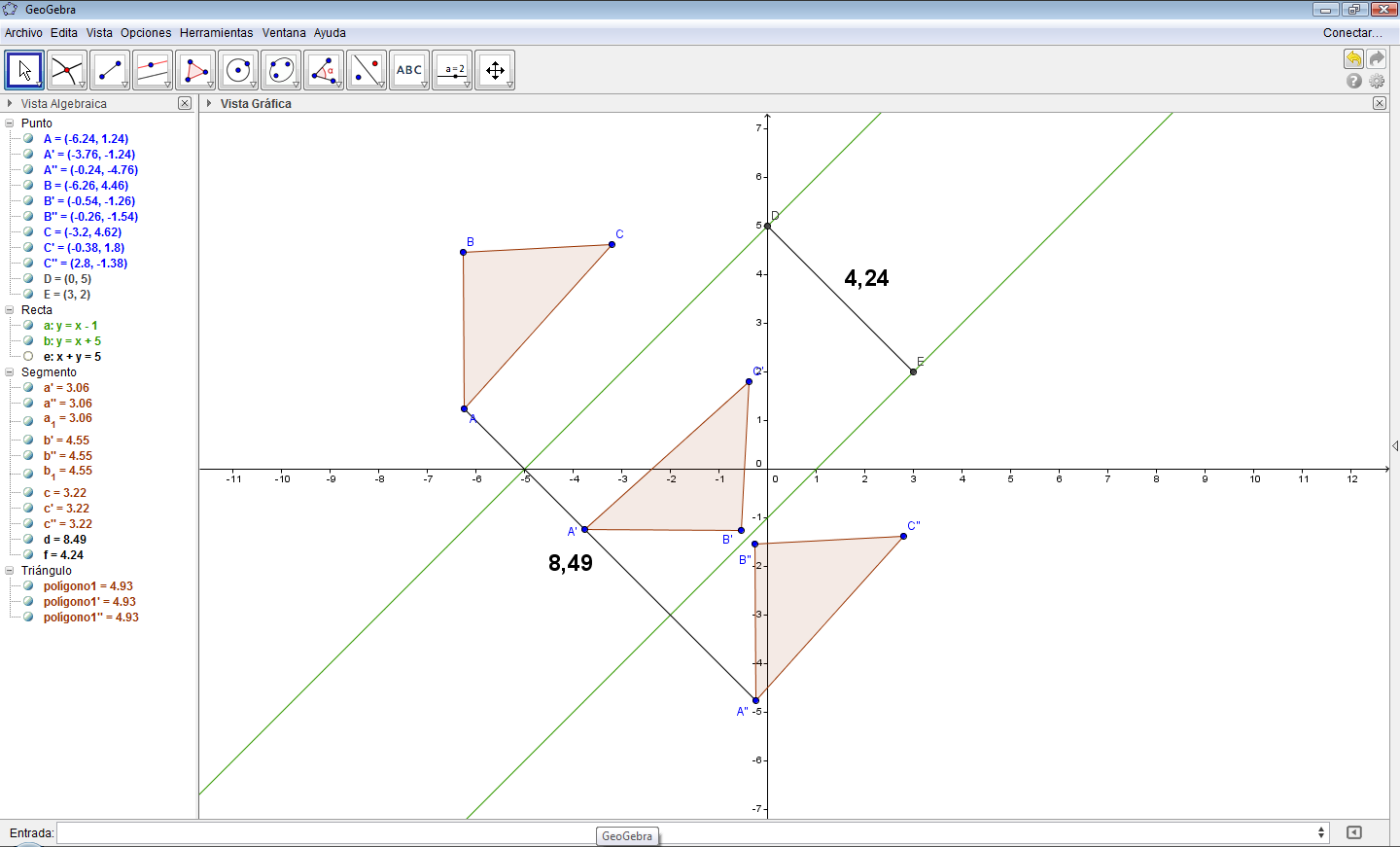 Fig. 98 Distancias de los triángulos
Fig. 98 Distancias de los triángulos Fig. 99 Construcción del codo circular
Fig. 99 Construcción del codo circular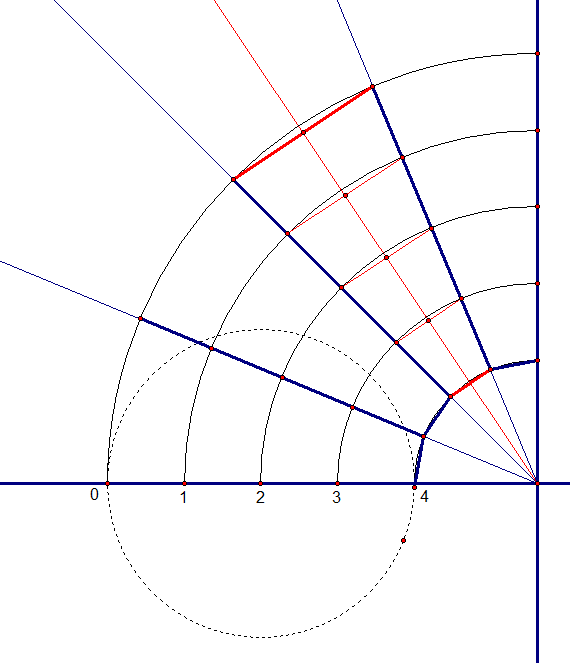 Fig. 100 Radios del codo con sus divisiones
Fig. 100 Radios del codo con sus divisiones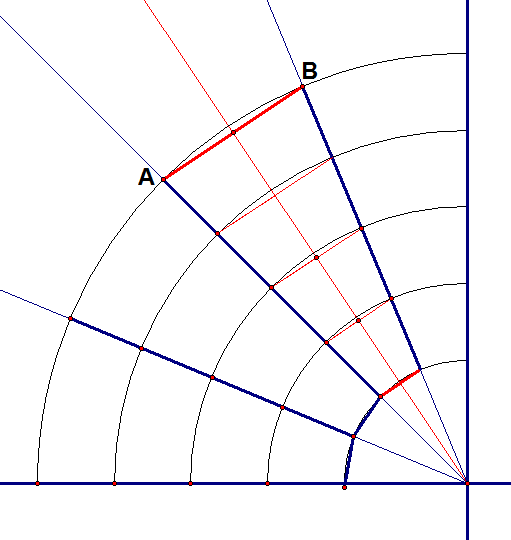 Fig. 101 Puntos A y B en el codo
Fig. 101 Puntos A y B en el codo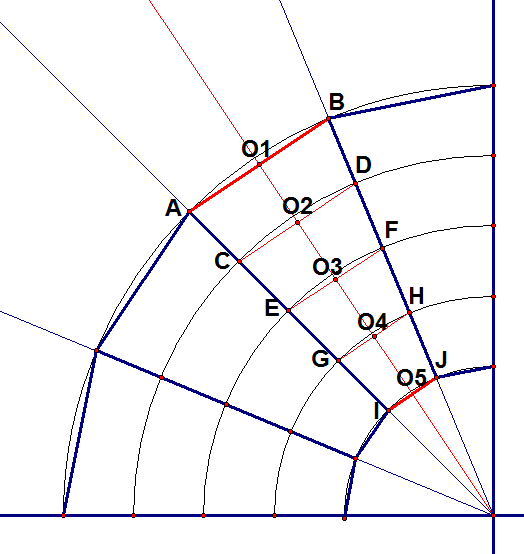 Fig. 102 Otros puntos en bisectrices consecutivas
Fig. 102 Otros puntos en bisectrices consecutivas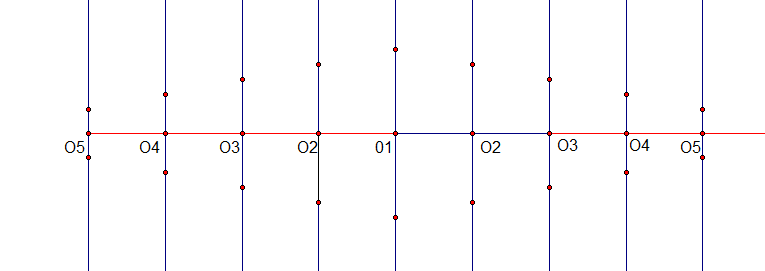 Fig. 103 Construcción de la plantilla a partir de los puntos en el codo
Fig. 103 Construcción de la plantilla a partir de los puntos en el codo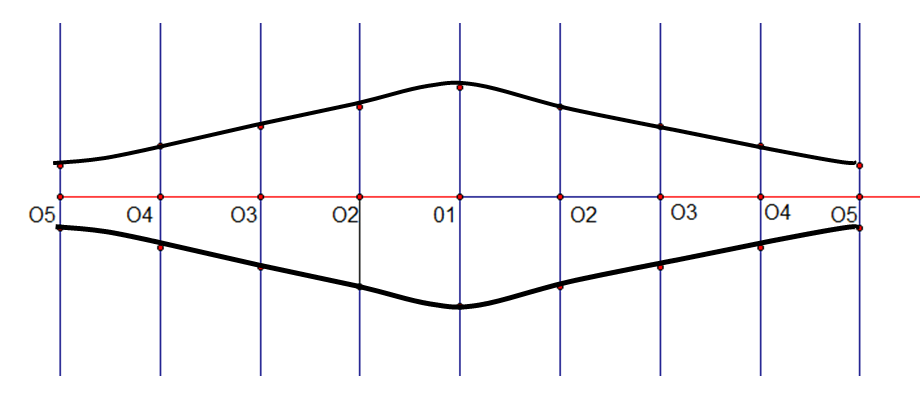 Fig. 104 Trazado de la plantilla
Fig. 104 Trazado de la plantilla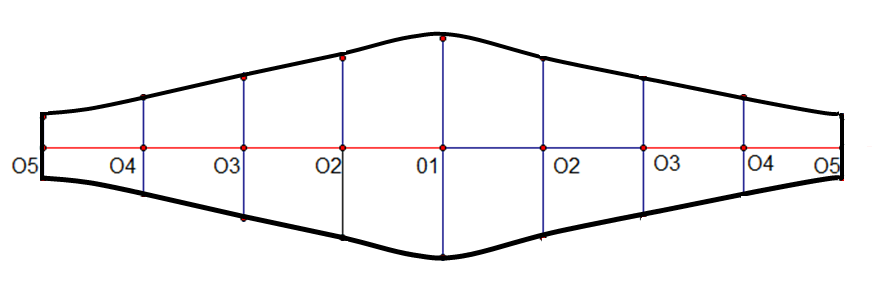 Fig. 105 Construcción de la plantilla
Fig. 105 Construcción de la plantilla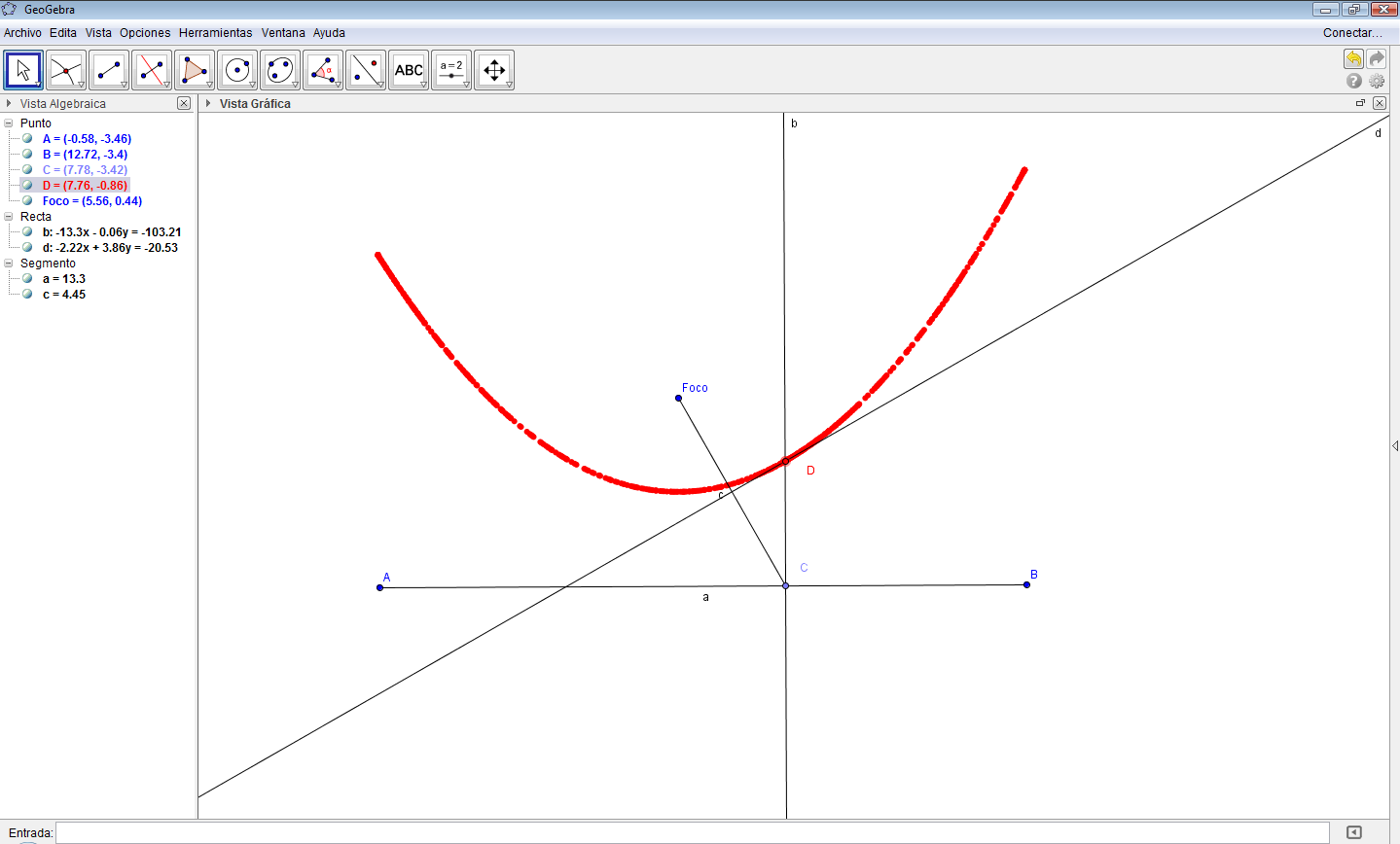 Fig. 106 Parábola en Geogebra
Fig. 106 Parábola en Geogebra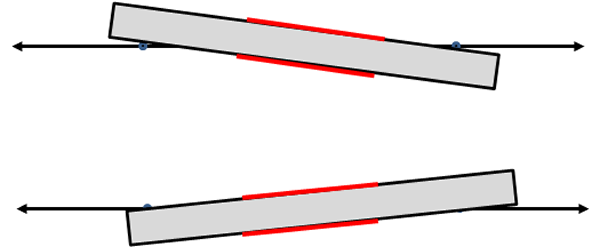 Fig. 107 Trazado de la mediatriz
Fig. 107 Trazado de la mediatriz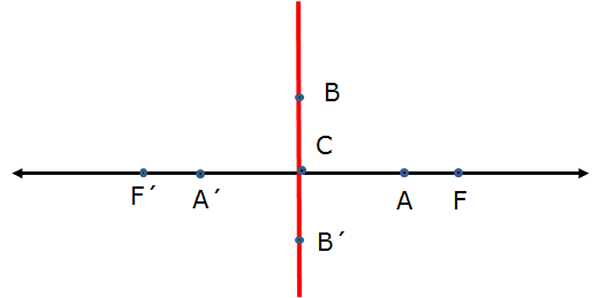 Fig. 108 Trazado de loa vértices
Fig. 108 Trazado de loa vértices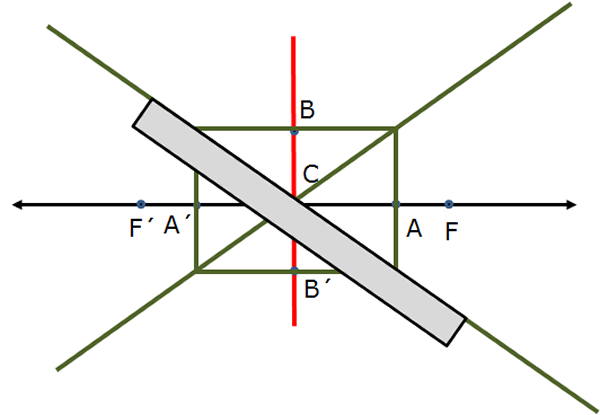 Fig. 109 Trazado del rectángulo
Fig. 109 Trazado del rectángulo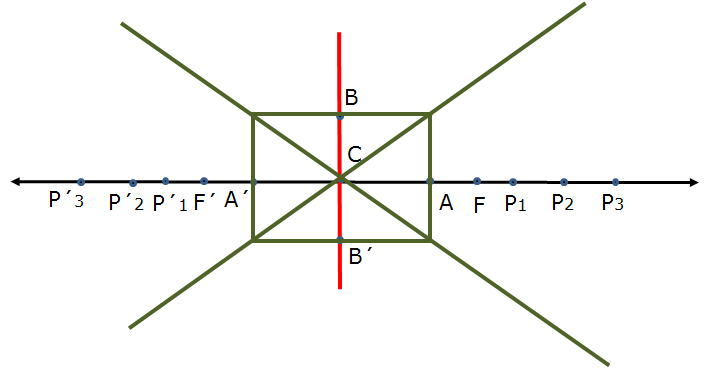 Fig. 110 Marcado de punto sobre la recta $l$
Fig. 110 Marcado de punto sobre la recta $l$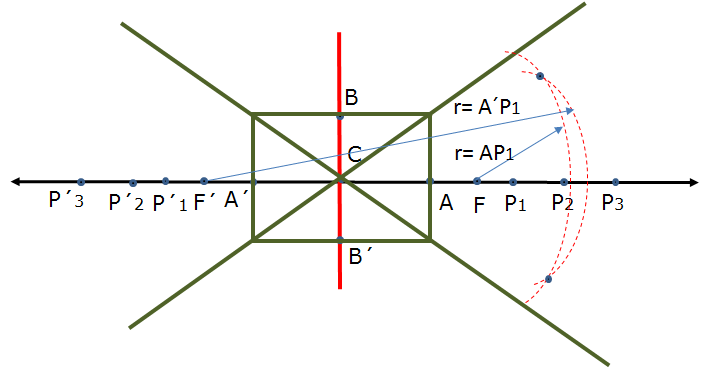 Fig. 111 Trazado de los arcos
Fig. 111 Trazado de los arcos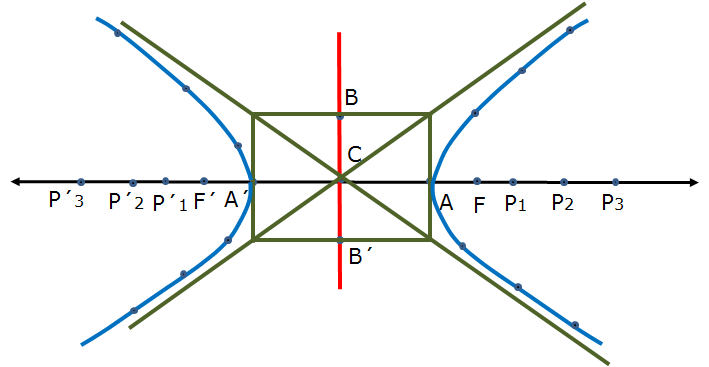 Fig. 112 Trazado de la hipérbola
Fig. 112 Trazado de la hipérbola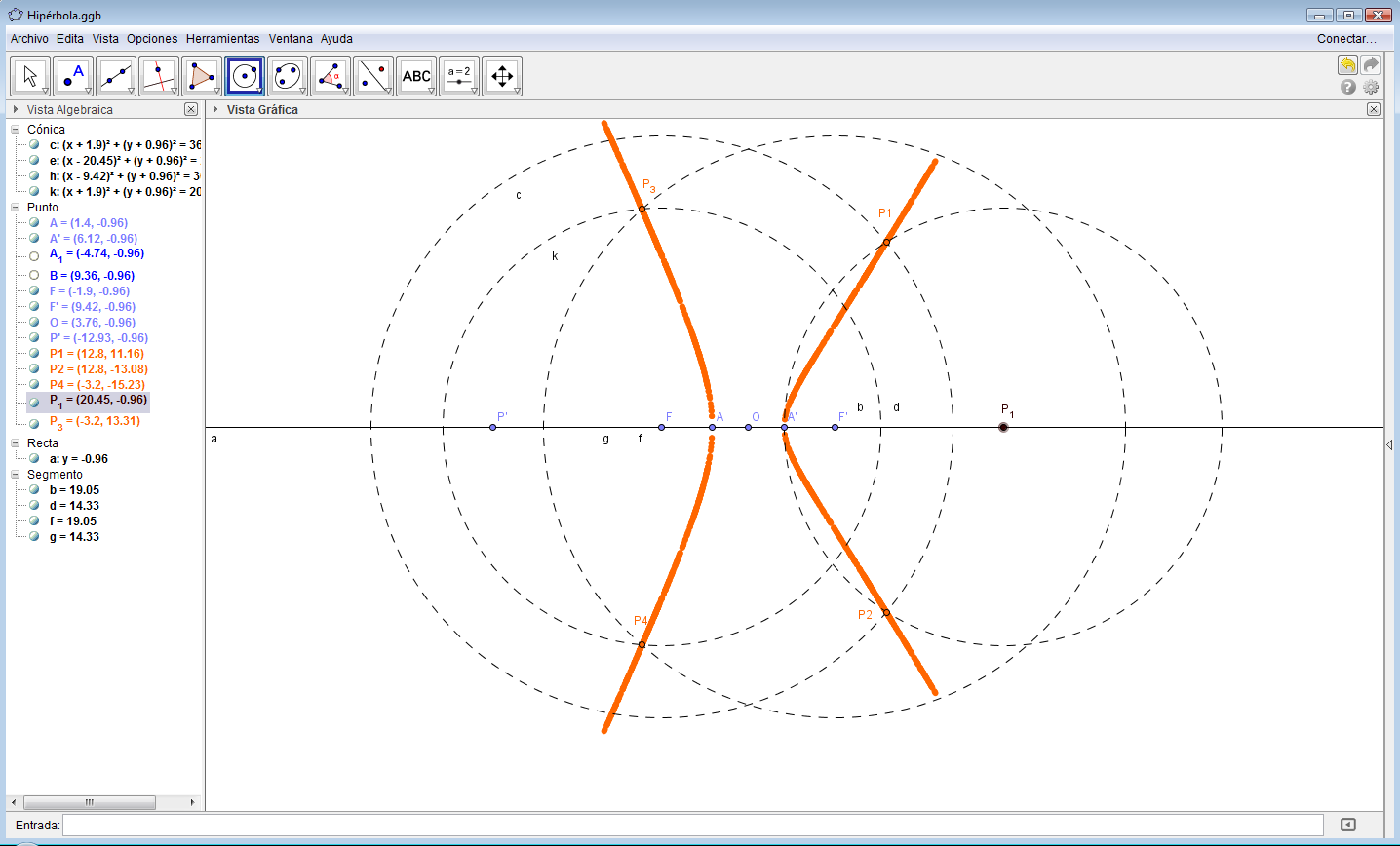 Fig. 113 Hipérbola en Geogebra
Fig. 113 Hipérbola en Geogebra