Regla y compás
Problemas de aplicación
Halmos, citado por Riverón Otoniel (s.f.), afirmó que “…resolver problemas es el corazón de las matemáticas” y Kleiner (1986) enfatizó que “…el desarrollo de conceptos y teorías matemáticas se originan a partir de un esfuerzo por resolver un determinado problema”.
Problemas tan famosos como por ejemplo la cuadratura del círculo, la trisección del ángulo y la duplicación del cubo enunciados por los griegos; el Teorema de los Cuatro Colores (resuelto por Appel y Kaken en 1976); el último Teorema de Fermat (resuelto por Wiles en 1994); la Conjetura de Goldbach; han sido la fuerza motriz para el desarrollo, no solo de la matemática, sino también de otras ciencias afines.
Es importante aprender a resolver problemas, buscar diferentes estrategias de solución y posibles respuestas, que permitan generar nuevo conocimiento, para el avance de la ciencia y la tecnología.
Problema
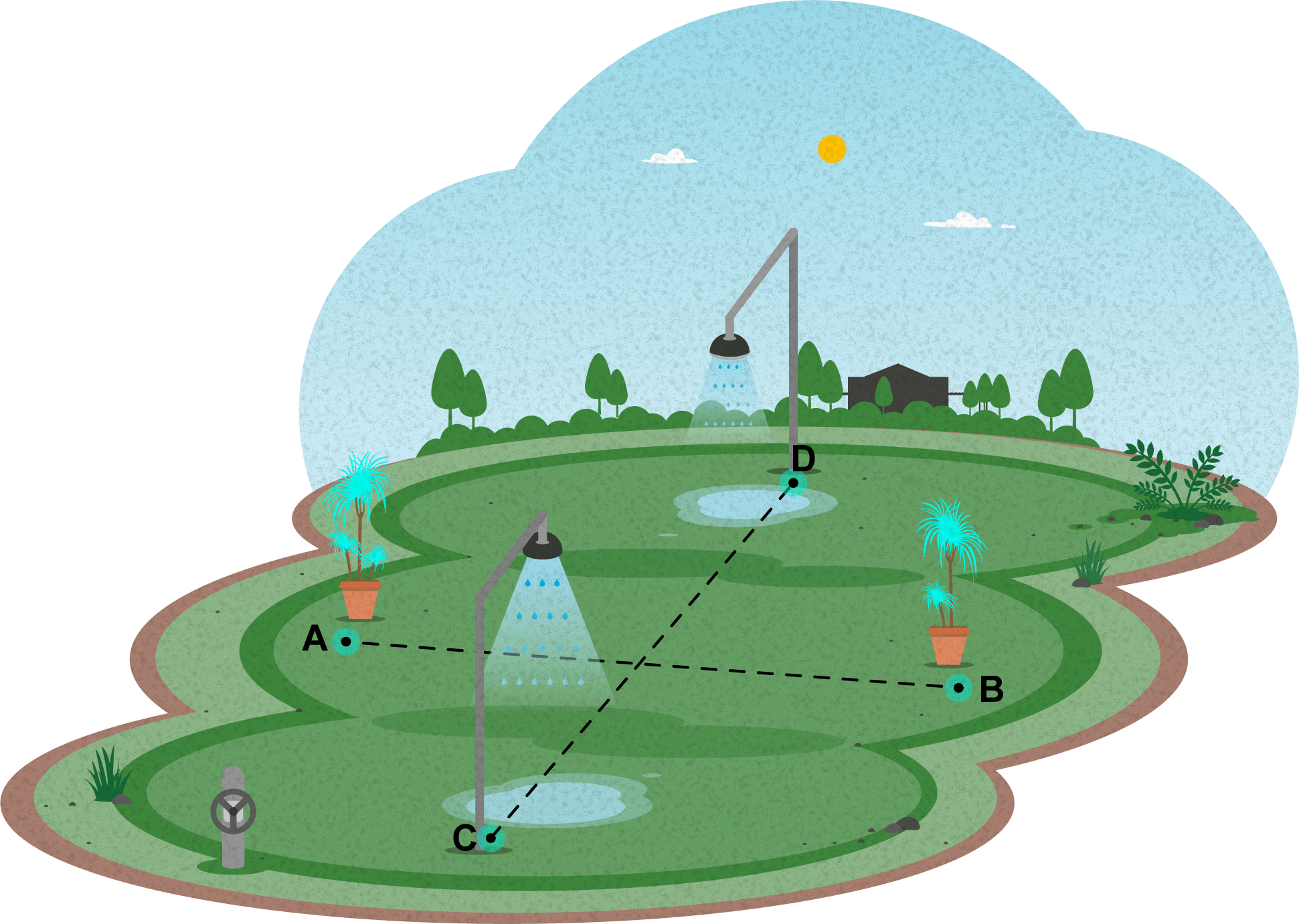
En la figura hay un rectángulo que representa un vivero, los puntos A y B corresponden a dos especies de plantas.
Se quiere colocar, en las paredes más largas del rectángulo, dos regaderas cuyas distancias, a las dos plantas, sean iguales.
Determine los puntos en los que deben colocarse las dos regaderas.
Solución
Trace la mediatriz del segmento determinado, por los puntos A y B.
C y D serán los puntos donde deben de colocarse las regaderas, en las paredes largas del rectángulo.
Todos los puntos de la mediatriz de un segmento equidistan de los extremos del segmento.
Problema

En el Canal de Panamá dos remolcadores tiran de un barco petrolero con igual fuerza. Para evitar una colisión, se separan formando un ángulo de 60◦. Determine la trayectoria del barco petrolero.
Solución
Los tres barcos son puntos del ángulo que mide 60◦, donde el vértice corresponde al barco petrolero.
Trace la bisectriz del ∠ABC y esa será la trayectoria del barco petrolero.
Problema
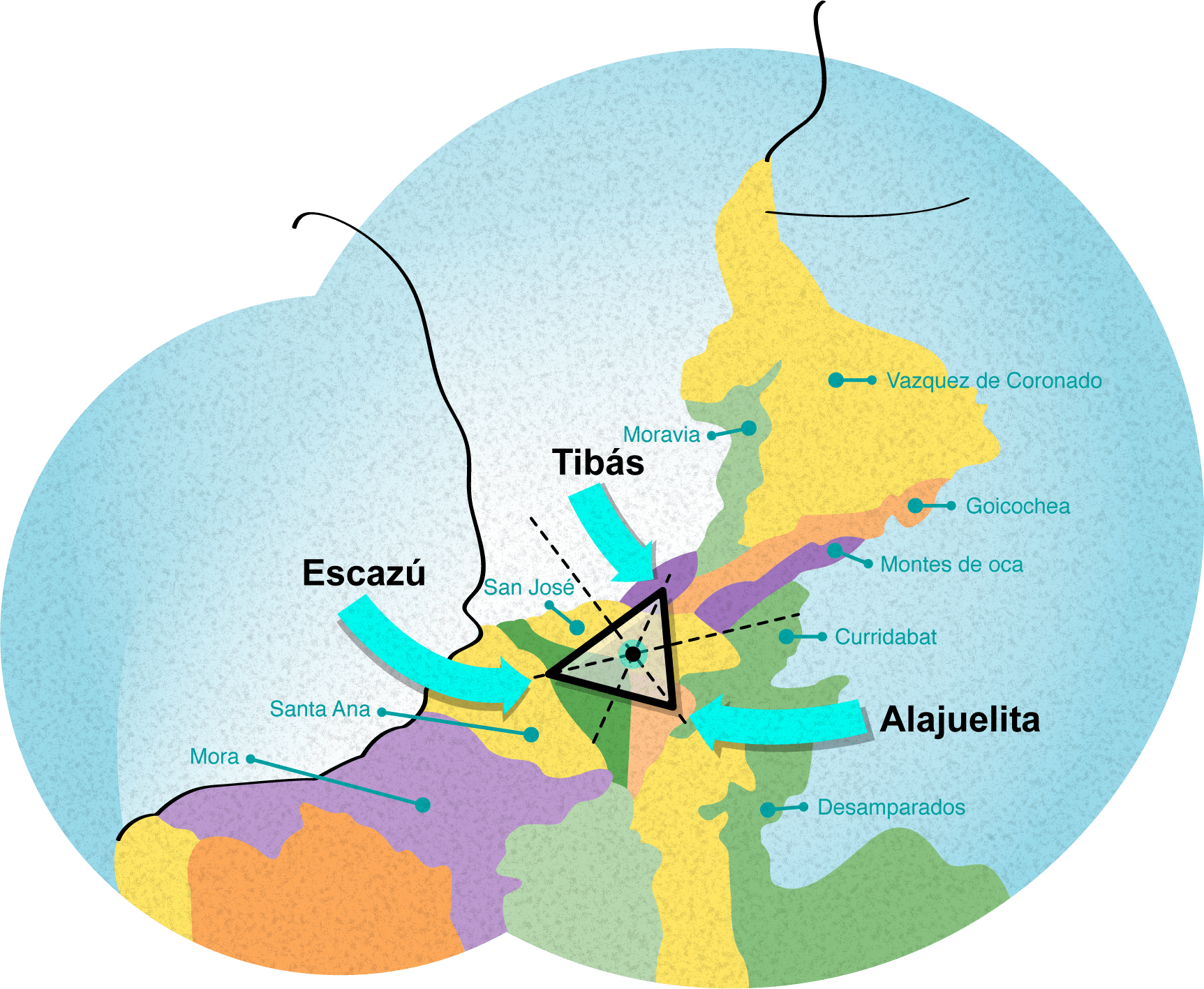
Suponga que el Ministerio de Obras Públicas y Transportes necesita construir una gran terminal de buses en la provincia de San José, que esté situada a la misma distancia de los centros de los cantones de Alajuelita, Tibás y Escazú. ¿En qué lugar debe ubicarse la terminal?
Solución
En la figura se muestra la ubicación de los tres cantones, en el mapa de la provincia de San José.
Sea A el punto donde se ubica el centro del cantón de Alajuelita, B el Tibás y C el de Escazú. De acuerdo con su ubicación en el mapa, estos tres puntos son no colineales, por lo tanto determinan el ABC.
Para encontrar la ubicación de la gran terminal de buses, basta con determinar el circuncentro del ABC.
El circuncentro es el punto de intersección de las tres mediatrices del triángulo y es el centro del círculo circunscrito a dicho triángulo.
El punto D será la ubicación de la terminal de buses pues $DA \cong DB \cong DC$ son radios del círculo. De acuerdo con el mapa, la terminal tendría que ubicarse en algún punto al sur del centro de San José.
Problema

Doña Lorena tiene un jardín en forma de cuadrilátero y desea construir otro en su interior, para sembrarlo con rosas de manera tal que su área sea igual a la mitad del área del jardín. ¿Cómo puede hacer esto doña Lorena?
Solución
En cualquier cuadrilátero, los puntos medios de los lados forman un paralelogramo cuya área es la mitad de la del cuadrilátero original. Por lo tanto, determine los puntos medios de los lados del jardín, estos serán los vértices del paralelogramo.
Para determinar los puntos medios, trace la mediatriz de cada uno de los lados del cuadrilátero.
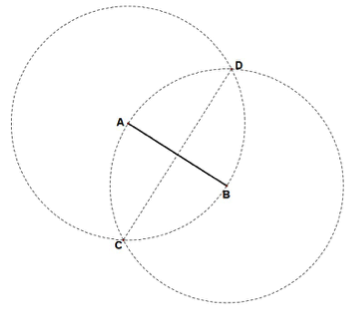 Fig. 17 Mediatriz de un segmento
Fig. 17 Mediatriz de un segmento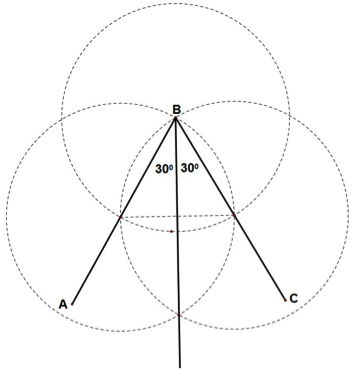 Fig. 19 Bisectriz de un ángulo
Fig. 19 Bisectriz de un ángulo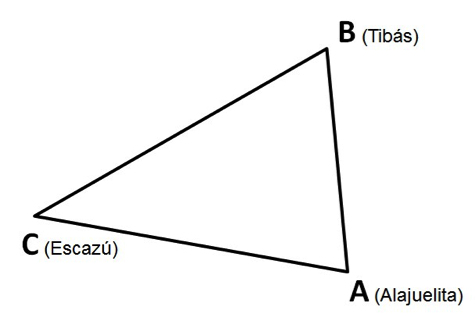 Fig. 21 Circuncentro
Fig. 21 Circuncentro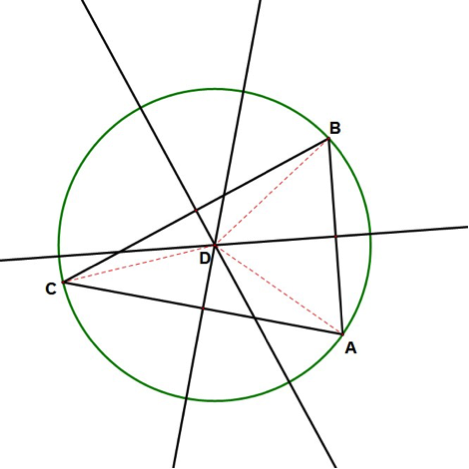 Fig. 22 Circuncentro
Fig. 22 Circuncentro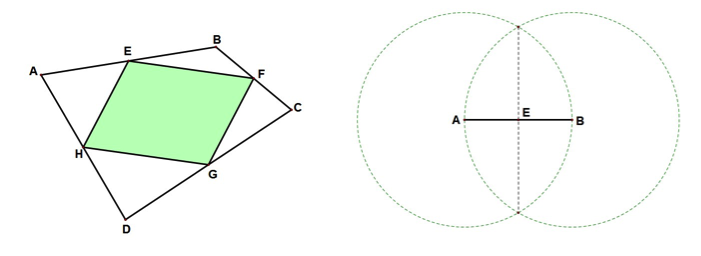 Fig. 24 Paralelogramo
Fig. 24 Paralelogramo