Doblado de papel
Problemas de aplicación
En geometría, como en cualquier otra situación de la vida, es importante aprender a observar cuidadosamente, escuchar con atención e interpretar las instrucciones para llevarlas a la práctica. Gracias a la papiroflexia u origami el estudiante puede interactuar directamente con muchos objetos matemáticos como: la diagonal, la mediana, los vértices, la bisectriz, entre otros.
De igual forma, tendrá una mejor visualización de los cuerpos geométricos y, por consecuencia, una buena compresión de sus propiedades. En este proceso de creación de las diferentes figuras, el estudiante además de fomentar la agilidad mental, también desarrolla estrategias para resolver problemas no solo de matemática, sino de la vida cotidiana. ¡Anímese y siga resolviendo problemas!Problema

Don José desea construir una mesa circular de $0,5 \;m$ de radio para exhibir unas orquídeas de su vivero. Con lo único que cuenta es con un pliego de papel cuadrado de $1,2 \;m$ de lado, una regla y unas tijeras. ¿Cómo podrías ayudar a don José a dibujar el círculo que necesita para construir su mesa circular?.
Solución
En la figura anterior se ilustra la mesa que desea construir don José.
- Trace los ejes de simetría y las diagonales, de la hoja de papel cuadrada.
- Trace la bisectriz de los ángulos $\angle FOB$ y $\angle BOG$.
- Repita el procedimiento anterior, para los otros tres cuadrantes del cuadrado.
- Dibuje un punto $X$, diferente del punto $O$, en cualesquiera de los dobleces, por ejemplo en el doblez $\overline{OF}$, tal que $OF=0,50\;m$.
- Traslade el punto $X$, para esto haga coincidir dos dobleces adyacentes.
- Repita el procedimiento anterior. A partir de este conjunto de puntos, se puede intuir la noción de circunferencia como: el conjunto de puntos del plano que equidistan de un punto fijo llamado centro.
- Finalmente, se puede trazar en forma aproximada la circunferencia y así don José podrá recortarla por su contorno y tener el “molde” para el sobre de su mesa circular.
Problema

Don Manuel quiere introducir una nueva línea de regaderas de base elíptica en su vivero, pero no sabe cómo hacer un molde en papel. Ayude a don Manuel a construir el molde en papel del tanque de la regadera.
Solución
En la figura anterior, se muestra el prototipo de la regadera que quiere construir don Manuel.
- Construya una elipse utilizando el doblado de papel (ver “Construcción de una elipse”) o haga uso de algún software (ver el laboratorio de “Otras herramientas”).
- Para determinar el largo del envolvente, marque un punto en el borde de la elipse y siga su contorno con un hilo, el largo del hilo es el perímetro de la elipse. (Para determinar el perímetro de una elipse se requiere del cálculo de integrales elípticas, que son integrales muy complicadas de calcular).
- Tome una hoja de papel rectangular, que tenga por largo la longitud del hilo y, por ancho, el alto de la hoja.
- Finalmente, ensamble el tanque con base elíptica, como se muestra en la figura.
Problema

Doña Lorena desea construir en su vivero un almácigo, cuyo techo tenga forma parabólica, pero no tiene idea de cómo se construye una parábola, ella solamente cuenta con un pliego de papel en forma rectangular. ¿Cómo podría doña Lorena construir un modelo para la parábola?.
Solución
En la figura anterior se muestra la situación planteada.
- Tome una hoja de papel rectangular y marque un punto F, cerca del borde inferior y, aproximadamente, a la mitad de la hoja.
- Doble el papel, de manera que un punto del borde inferior coincida sobre el punto F .
- Marque el doblez.
- Repita el procedimiento anterior. A partir de este conjunto de puntos, se puede intuir la noción de parábola como: el conjunto de puntos del plano que equidistan de un punto fijo, llamado foco y, una recta, llamada directriz.
Problema

Don Juan quiere construir maceteras en forma de cubo truncado. Ayude a don Juan a construir un modelo para su macetera.
Solución
En la figura anterior se muestra la situación planteada.
- El cubo truncado es un prisma formado por seis octógonos regulares y ocho triángulos equiláteros.
- Construya un octógono regular (ver construcción del “Octógono regular”).
- Construya un triángulo equilátero (ver construcción “Ángulos de $15^{\circ}$, $30^{\circ}$ y $60^{\circ}$”).
- Construya un molde como el de la figura y dóblelo por las líneas punteadas, para obtener el cubo truncado.
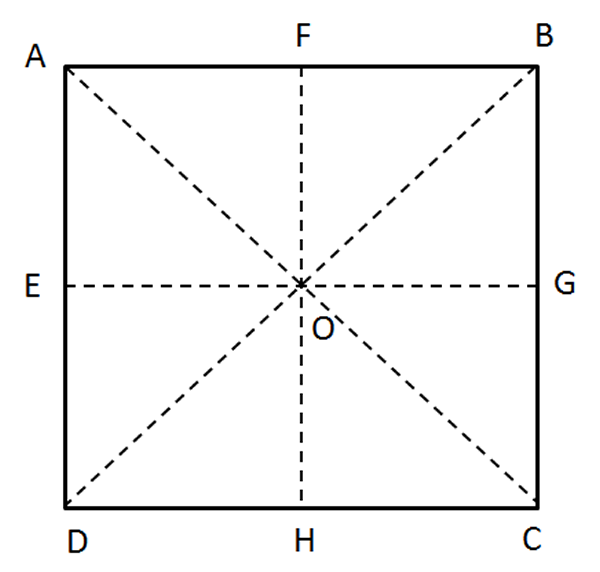 Fig. 75 Ejes de simetría y diagonales
Fig. 75 Ejes de simetría y diagonales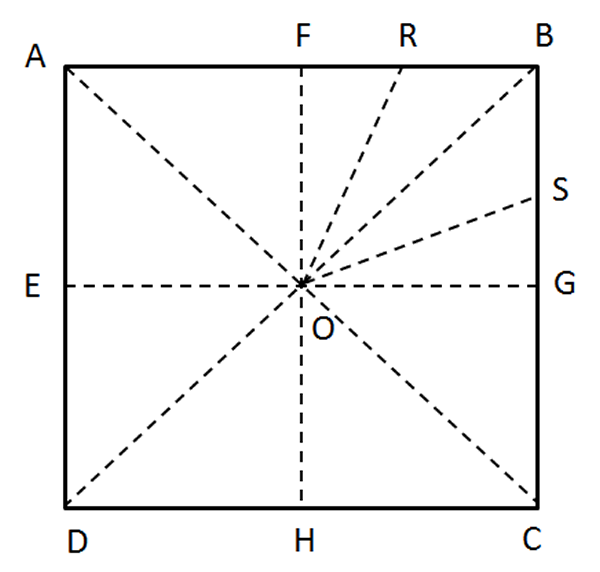 Fig. 76 Bisectrices
Fig. 76 Bisectrices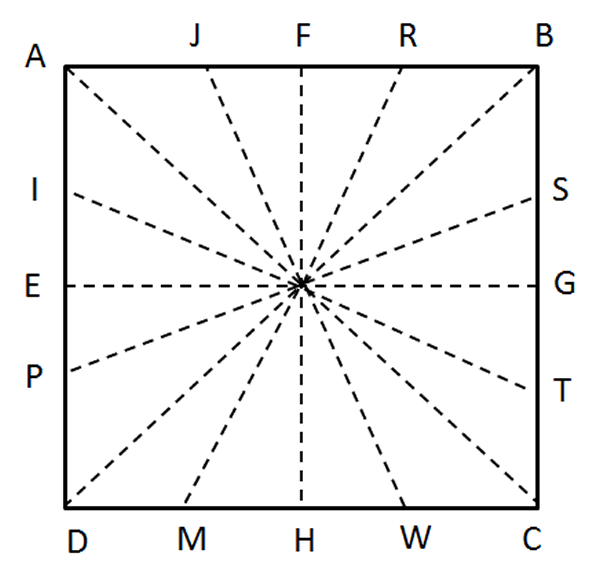 Fig. 77 Todas las bisectrices
Fig. 77 Todas las bisectrices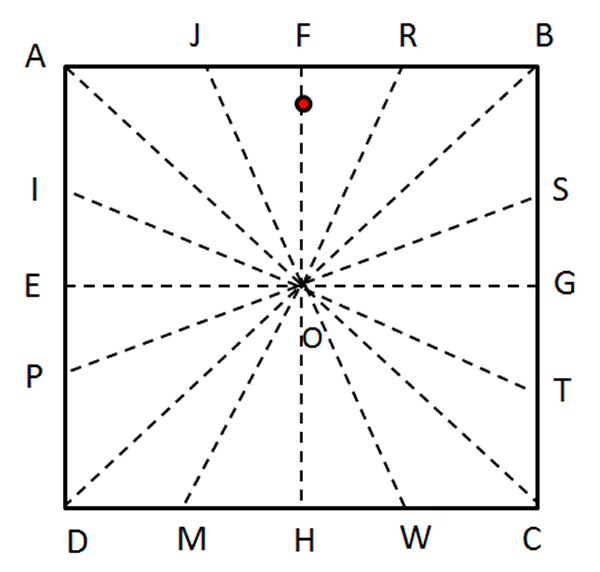 Fig. 78 El punto $X$
Fig. 78 El punto $X$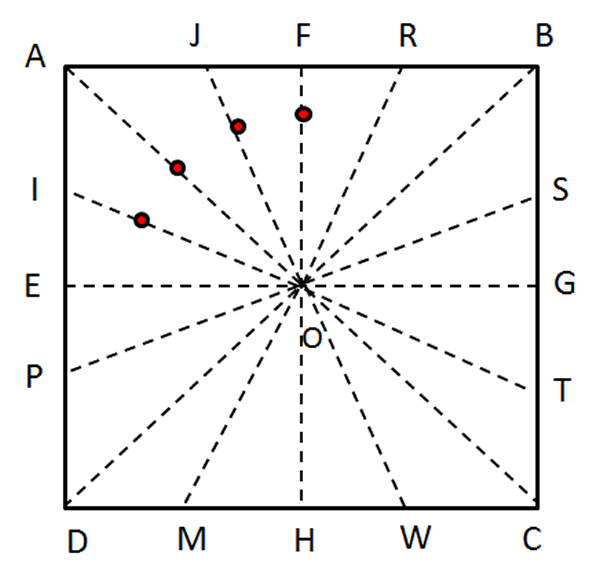 Fig. 79 Traslación del punto $X$
Fig. 79 Traslación del punto $X$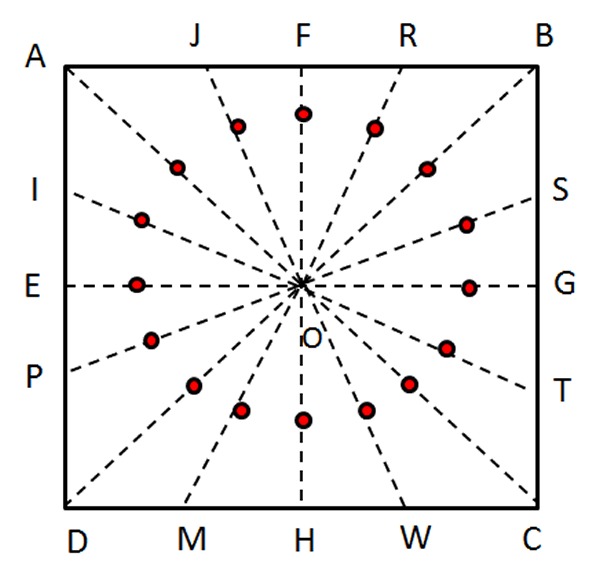 Fig. 80 Todos los puntos equidistantes del punto centro
Fig. 80 Todos los puntos equidistantes del punto centro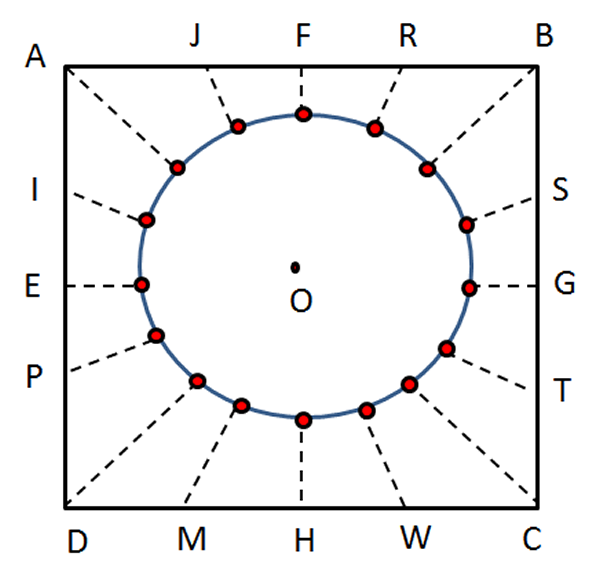 Fig. 81 Circunferencia deseada
Fig. 81 Circunferencia deseada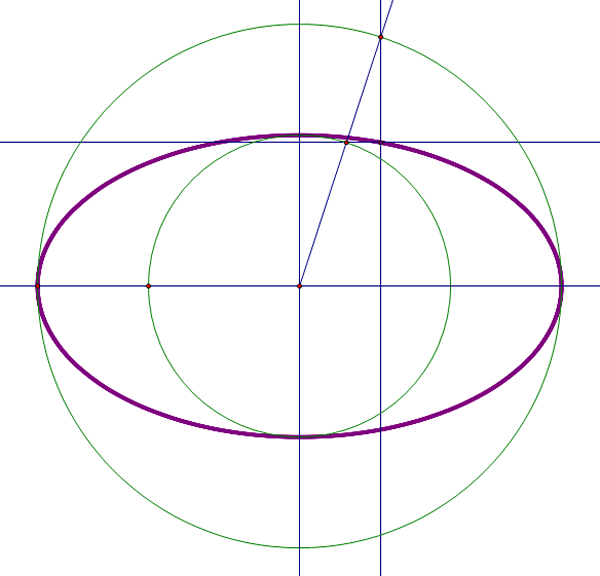 Fig. 83 Elipse
Fig. 83 Elipse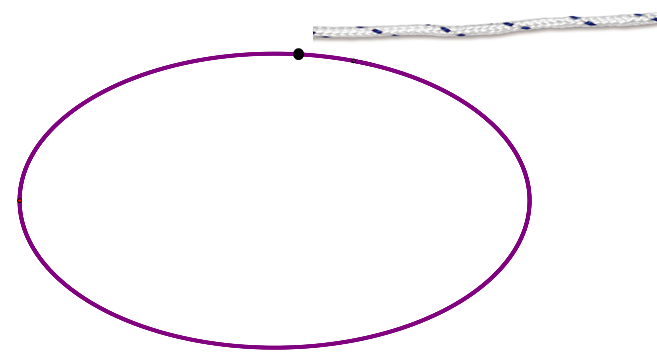 Fig. 84 Contorno de la elipse
Fig. 84 Contorno de la elipse Fig. 85 Hoja de papel rectangular
Fig. 85 Hoja de papel rectangular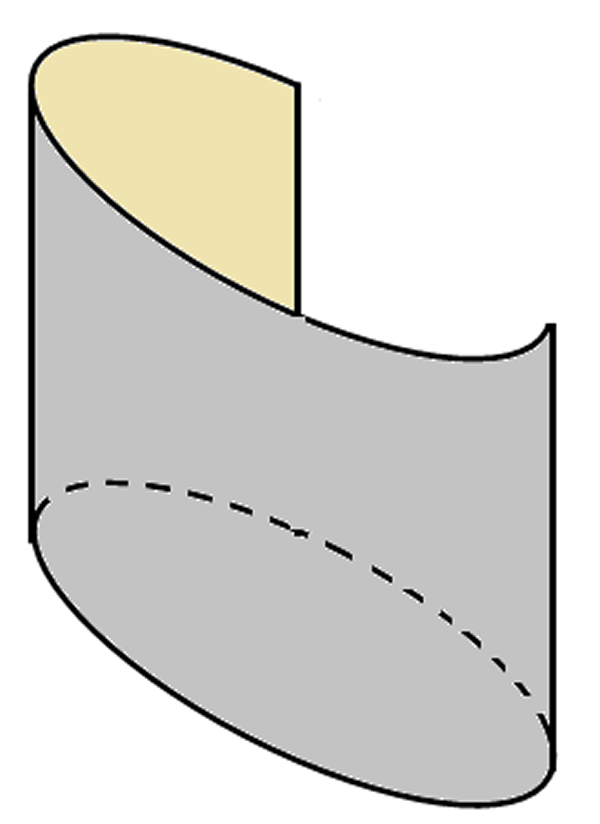 Fig. 86 Ensamble del tanque
Fig. 86 Ensamble del tanque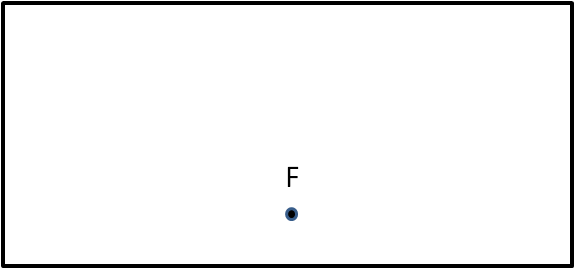 Fig. 88 Marcado del punto $F$
Fig. 88 Marcado del punto $F$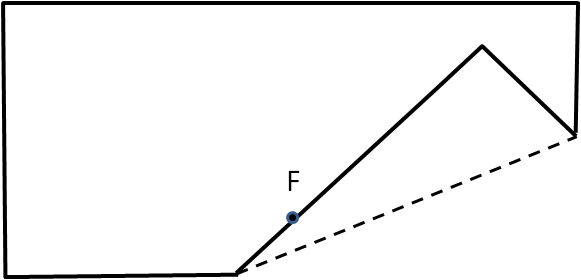 Fig. 89 Doblado del papel
Fig. 89 Doblado del papel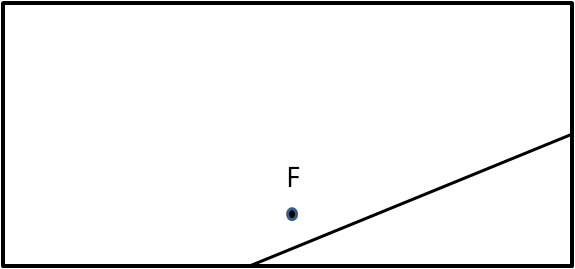 Fig. 90 Marcado del papel
Fig. 90 Marcado del papel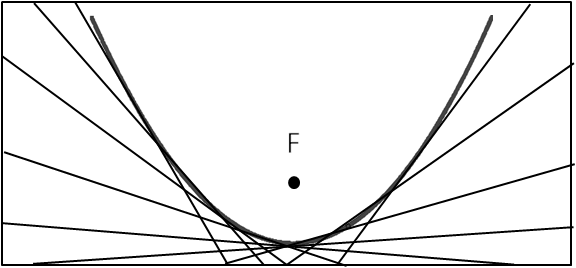 Fig. 91 Varias marcas de doble en el papel
Fig. 91 Varias marcas de doble en el papel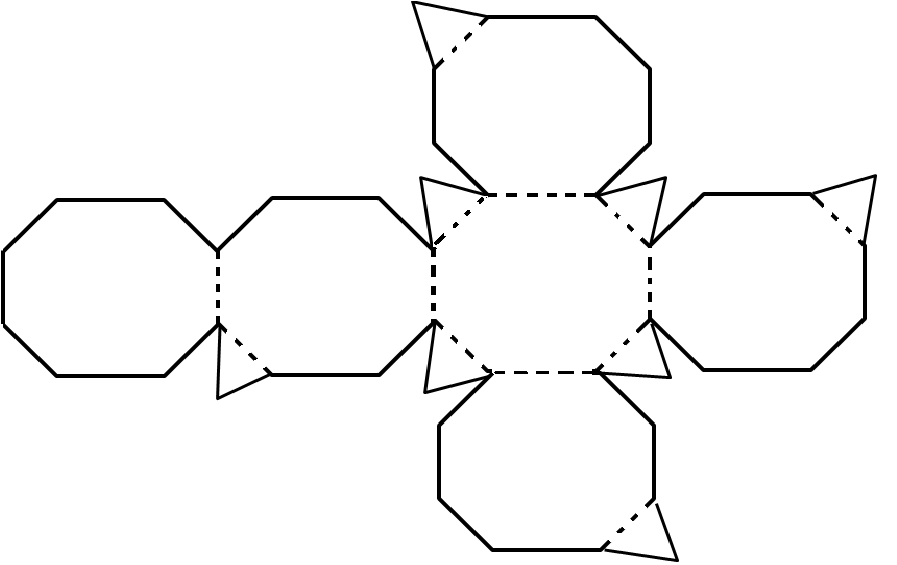 Fig. 93 Cubo truncado
Fig. 93 Cubo truncado