Portasegmentos
Problemas de aplicación
Resolver problemas es primordial en la enseñanza y aprendizaje de la matemática, ya que, además de ser una excelente estrategia didáctica, permite que, con una buena mediación pedagógica de los contenidos por parte del docente, el estudiante pueda alcanzar los objetivos propuestos. Por eso, para resolver problemas, hay que tomar en cuenta el interés del estudiante, tener presente que muchas veces no existe solo un camino para su solución y, lo más importante, el deseo de resolver el problema y afrontar el reto.
Allan Schoenfeld, matemático norteamericano, también señala que las creencias sobre la matemática influyen, en forma notable, en la forma en que, tanto estudiantes como profesores, abordan la resolución de un problema. Así que, ¡anímese a resolver problemas!
Problema
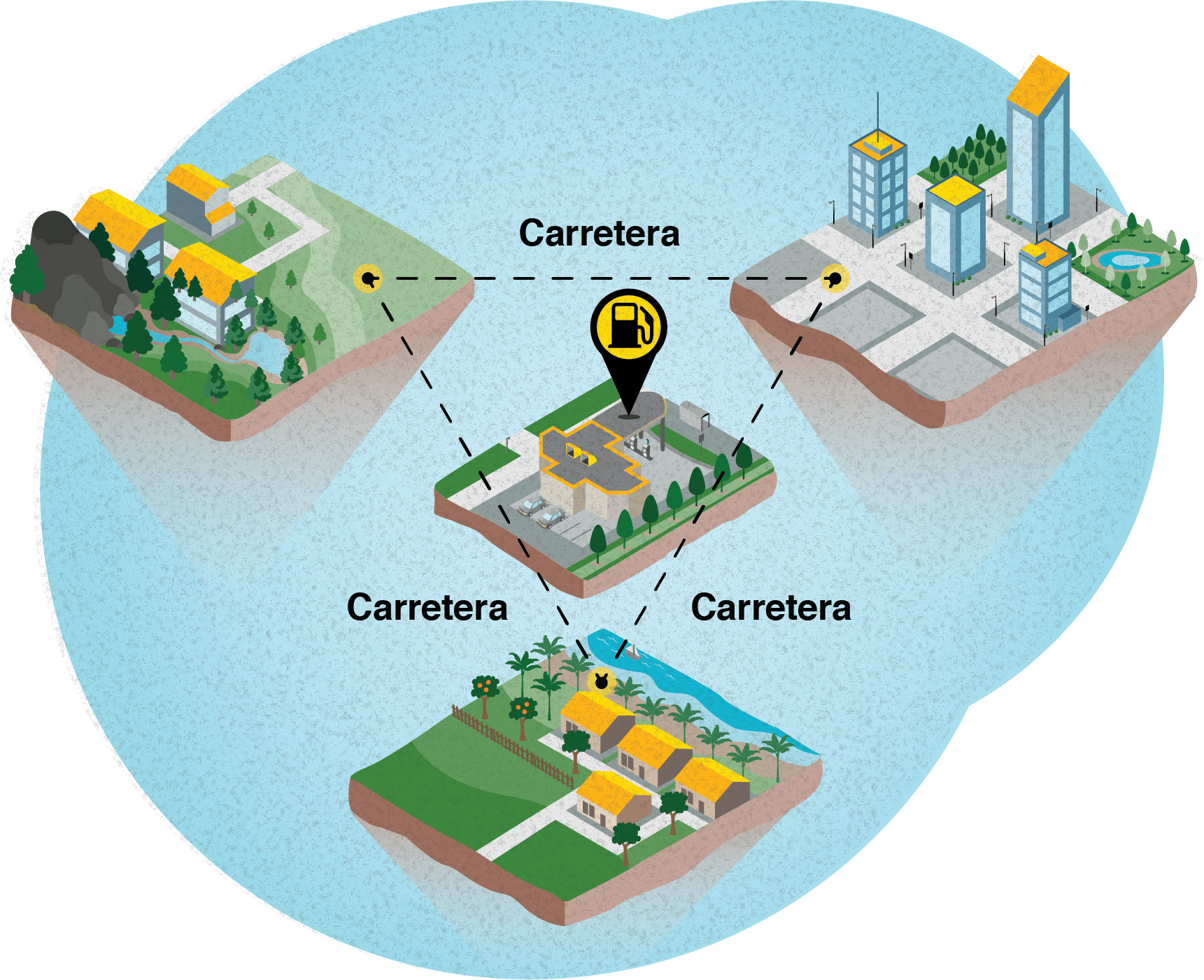
Tres pueblos están unidos por tres carreteras. Las municipalidades se han puesto de acuerdo para construir una estación de gasolina que se ubique a la menor distancia de las tres carreteras. ¿Dónde se tiene que ubicar la gasolinera?
Solución
En la figura anterior se ilustra la situación planteada.
Los tres pueblos se ubican en los vértices de un triángulo. Entonces:
- Construya, con el portasegmentos, el $\triangle ABC$.
- Trace las bisectrices de cada uno de los ángulos internos del triángulo.
- El punto de intersección de las bisectrices es el incentro (centro de la circunferencia inscrita en el triángulo).
- $\overline{OA}\cong \overline{OB}\cong \overline{OC}$ son radios del círculo y perpendiculares a los lados del triángulo.
La menor distancia de un punto a una recta es el segmento perpendicular. Por lo tanto, la gasolinera tiene que colocarse en el incentro del triángulo, cuyos vértices son los tres pueblos.
Problema

En un vivero se quiere construir un estanque que tenga forma elíptica. El capataz no tiene un compás para poder trazar la elipse, solamente cuenta con una regla y una cinta métrica. ¿Cómo podrías ayudar al capataz a trazar la elipse?
Solución
En la figura anterior se muestra la elipse que tiene que trazar el capataz.
En este caso, el capataz puede usar la regla como portasegmentos y con la cinta métrica tomar la medida de los dos ejes.
- Trace la recta $x$ y sobre ella marque el segmento $\overline{MN}$, que será el eje mayor.
- Trace la mediatriz del segmento $\overline{MN}$ y denote, con $O$, el punto medio.
- Sobre la mediatriz tome, con el portasegmentos, la distancia $d(OP)=d(OQ)$, igual a la medida del semieje menor.
- Sobre el portasegmentos, marque los puntos $B$, $C$ y $A$, en ese orden, de manera que $AB=\frac{MN}{2}$ y $AC=\frac{PQ}{2}$.
- Mueva el portasegmentos, de modo que $B$ quede siempre sobre el eje menor y $C$ sobre el eje mayor. El punto $A$, marcado sobre el portasegmentos, irá determinando los puntos de la elipse.
- Finalmente, con una curva suave dibuje la elipse.
Problema

En una finca se tienen tres plantaciones de árboles frutales que no están en línea recta. Se quiere colocar una llave de riego, de tal manera que se encuentre a la misma distancia de las tres plantaciones. ¿En qué lugar se tiene que colocar la llave de riego?
Solución
En la figura anterior se ilustra la situación planteada.
- Marque con $A$, $B$ y $C$, los puntos de ubicación de las tres plantaciones y trace con el portasegmentos la mediatriz de los segmentos $\overline{AB}$ y $\overline{BC}$.
- Denomine, con la letra $O$, al punto de intersección de las dos mediatrices.
- En el punto $O$ se debe colocar la llave de riego. Este punto se llama circuncentro del $\triangle ABC$.
Problema
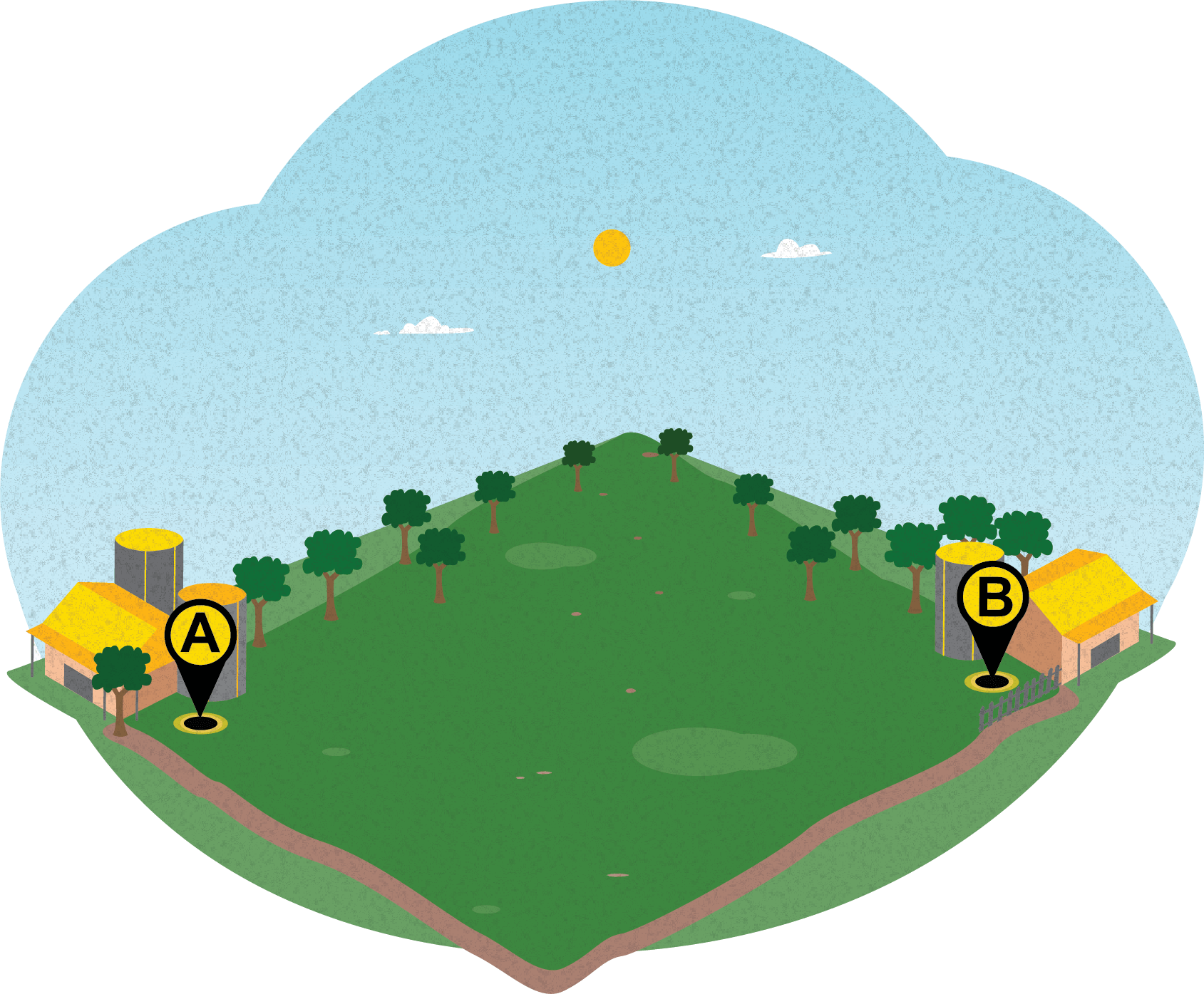
En una finca se tienen dos bodegas, donde se almacena el alimento para los animales. Se quiere trazar un camino, de tal manera que la distancia de cualquier punto del camino a cada una de las bodegas sea la misma. ¿Dónde se tiene que ubicar el camino?
Solución
En la figura anterior se ilustra la situación planteada.
- Trace, con el portasegmentos, la mediatriz del segmento $\overline{AB}$.
- Por la mediatriz hay que trazar el camino, ya que todos los puntos de la mediatriz equidistan de los extremos del segmento.
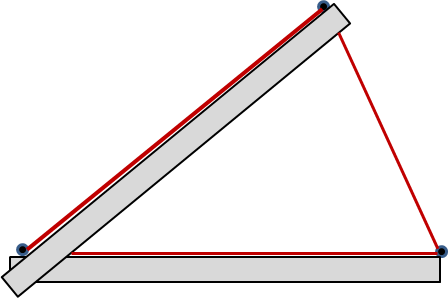 Fig. 35 Construir el triángulo
Fig. 35 Construir el triángulo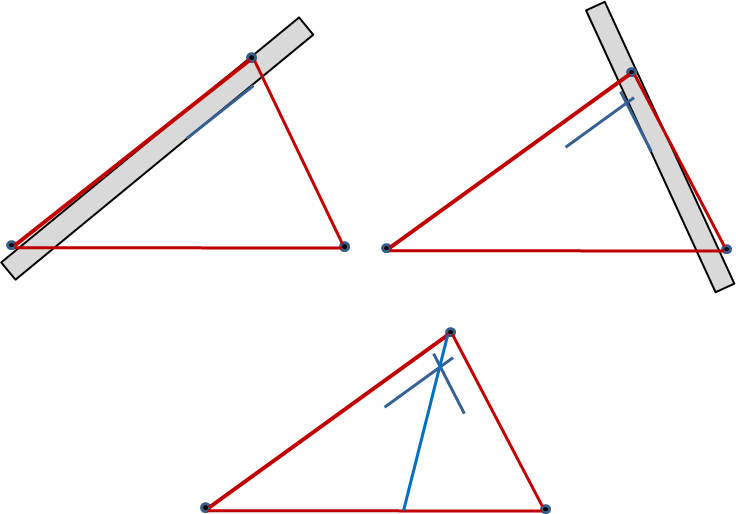 Fig. 36 Trazado de las bisectrices
Fig. 36 Trazado de las bisectrices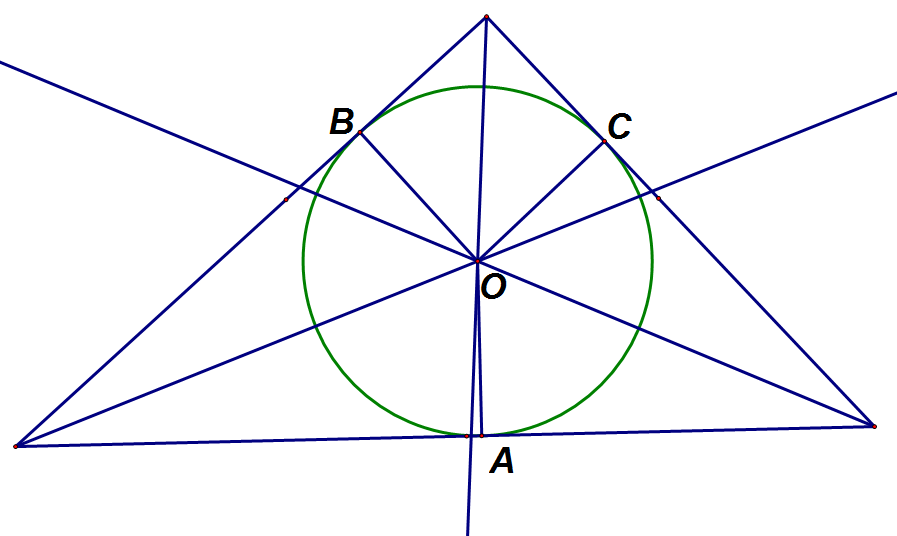 Fig. 37 Punto de intersección
Fig. 37 Punto de intersección Fig. 39 Trazado de la recta
Fig. 39 Trazado de la recta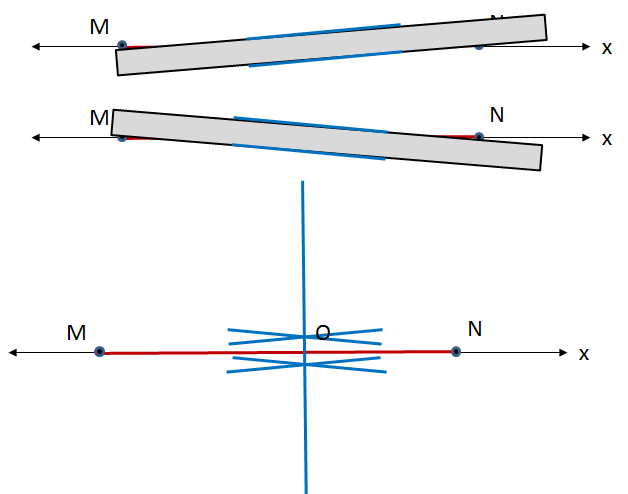 Fig. 40 Trazado de la mediatriz
Fig. 40 Trazado de la mediatriz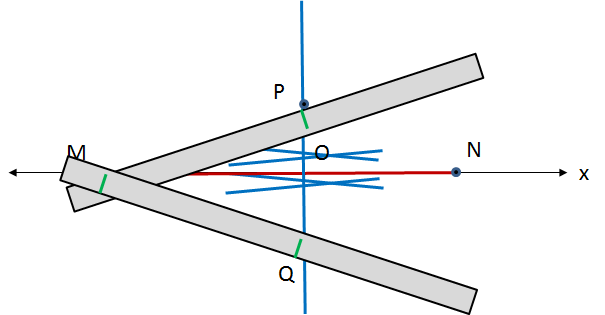 Fig. 41 El semieje menor
Fig. 41 El semieje menor Fig. 42 Marcado del portasegmentos
Fig. 42 Marcado del portasegmentos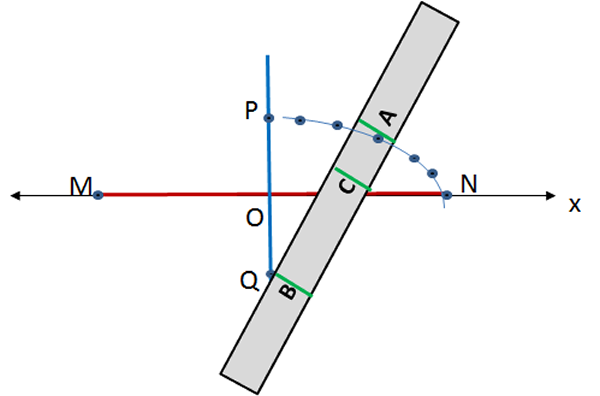 Fig. 43 Determinar los puntos de la elipse
Fig. 43 Determinar los puntos de la elipse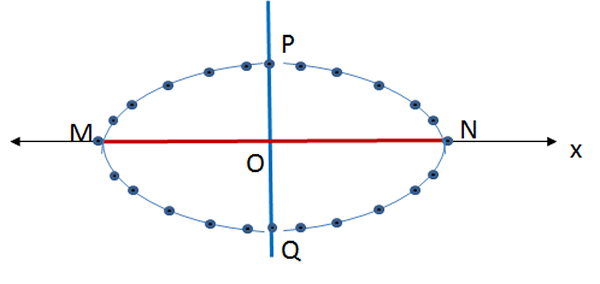 Fig. 44 Trazado de la elipse
Fig. 44 Trazado de la elipse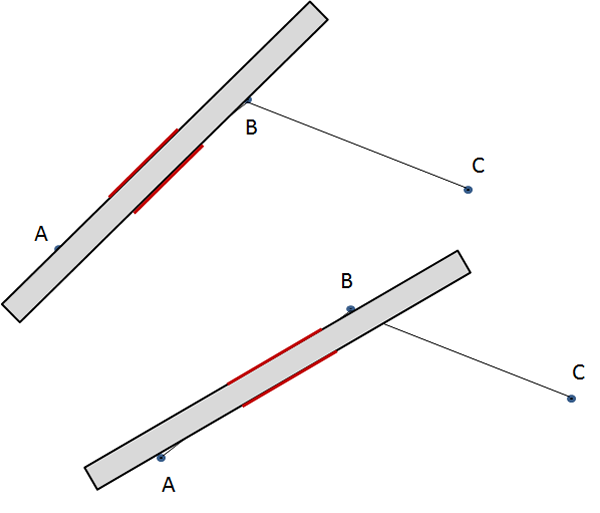 Fig. 46 Ubicación de las tres plantaciones
Fig. 46 Ubicación de las tres plantaciones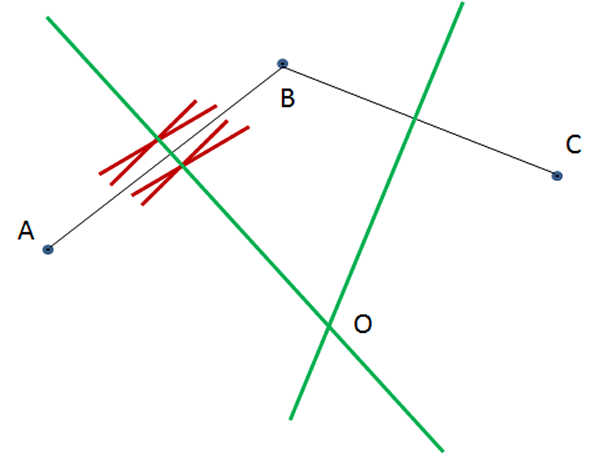 Fig. 47 Intersección de las dos mediatrices
Fig. 47 Intersección de las dos mediatrices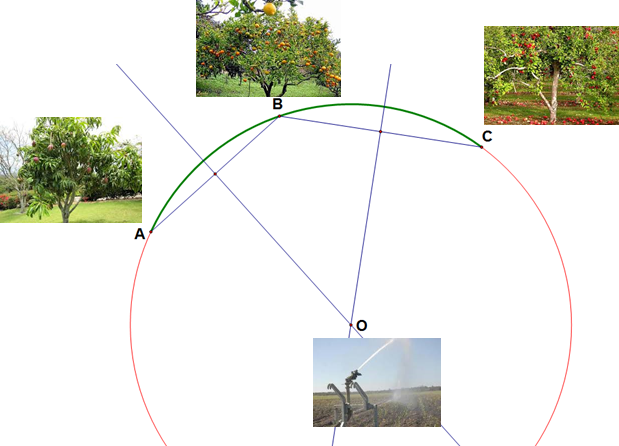 Fig. 48 Circuncentro
Fig. 48 Circuncentro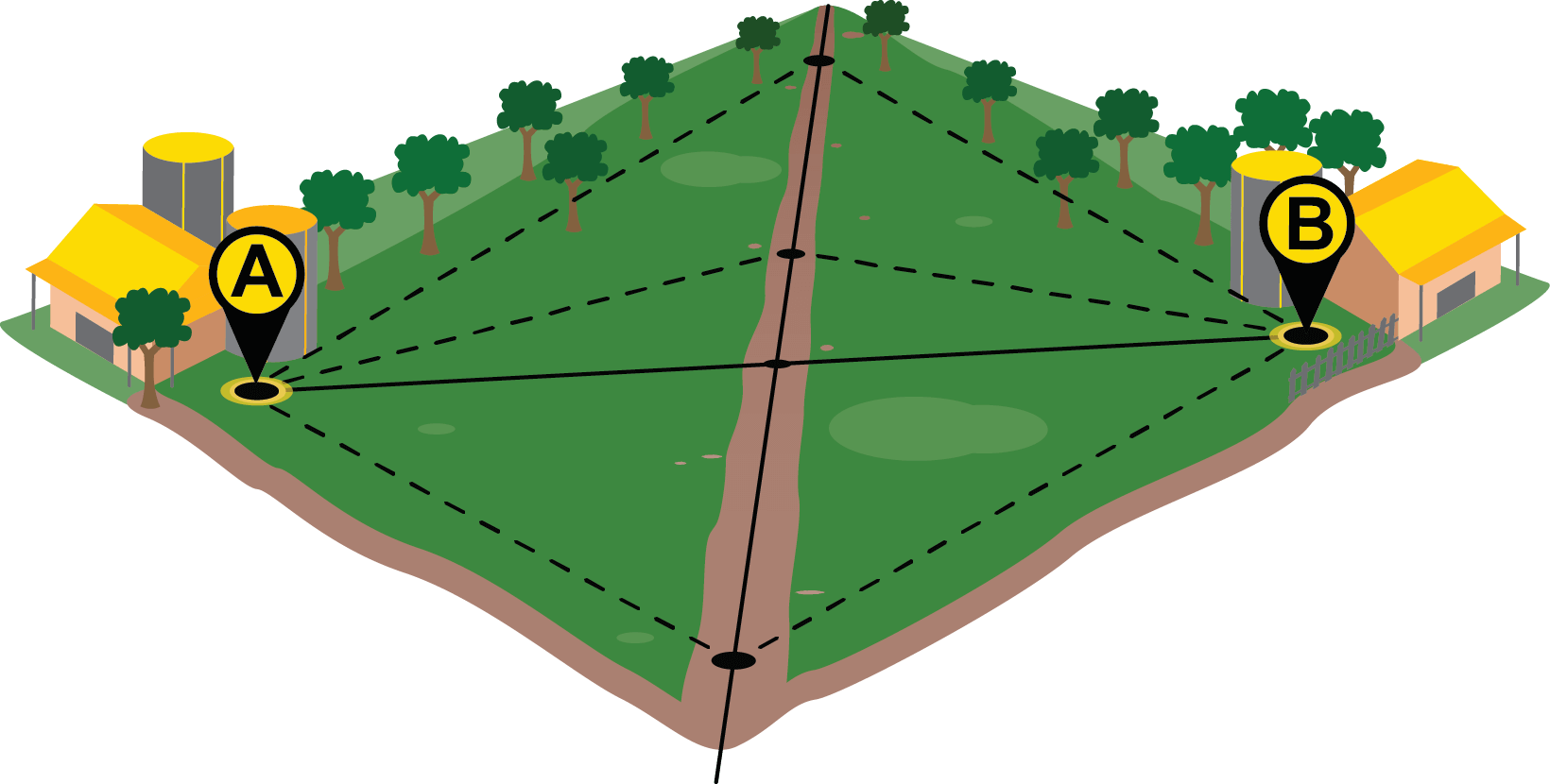 Fig. 50 Mediatriz
Fig. 50 Mediatriz