Portasegmentos
Construcciones
Con el portasegmentos, también, se pueden lograr construcciones geométricas nítidas y claras, de la misma forma que cuando se utiliza la regla y el compás, solamente se ocupa un poco de precisión y cierto grado de habilidad.
Las construcciones geométricas, que se presentan a continuación, son muy sencillas, algunas ya fueron construidas con la regla y el compás (ver laboratorio de construcciones geométricas con regla y compás).
Si su portasegmentos no está construido con un material duradero, es necesario que tenga varios a mano, pues se deterioran con facilidad. Para realizar estas construcciones es necesario saber:
- Comparar segmentos.
- Reconocer segmentos consecutivos colineales.
- Expresar la longitud de un segmento, tomando como unidad la medida de otro segmento.
- Realizar operaciones con segmentos: suma, resta, multiplicación por un número racional, producto de medidas de segmentos, división de segmentos por un número racional.
Ahora, tome su portasegmentos y haga las construcciones que se muestran en este multimedia. ¡Anímese!
Procedimiento
- Trace la recta $x$ y sobre ella marque el segmento $\overline{AB}$.
- Haga coincidir los lados del portasegmentos con los extremos del segmento dado y trace una línea a cada lado del portasegmentos. Repita el procedimiento, pero ahora en dirección contraria y trace nuevamente las líneas a cada lado del portasegmento, como se muestra en la figura.
- Marque los puntos $C$ y $D$ los cuales pertenecerán a la mediatriz del segmento $\overline{AB}$.
- Trace la recta que pasa por los puntos $C$ y $D$, esta es la mediatriz.
Propiedad
La mediatriz de un segmento es la bisectriz perpendicular de dicho segmento.
Procedimiento
- Trace la recta $m$ y sobre ella marque el segmento $\overline{AB}$, tal que $AB=a$.
- Trace la mediatriz del segmento $\overline{AB}$.
- Trace los segmentos $\overline{AC'}$ y $\overline{BC'}$ de longitud $a$.
- El $\triangle ABC'$ es equilátero, cuya altura mide $\frac{a\sqrt{3}}{2}$.
- Prolongue la altura del triángulo y, sobre la prolongación, marque el segmento $\overline{C'D}$ de longitud $\frac{a\sqrt{3}}{2}$.
- $CD =CC'+C'D$, por suma de segmentos.
- $CD=\frac{a\sqrt{3}}{2}+\frac{a\sqrt{3}}{2}=a\sqrt{3}$.
Propiedad
El área de un triángulo equilátero de lado $l$, viene dada por la fórmula $A=\frac{l^2\sqrt{3}}{4}$.
Procedimiento
- Trace la recta $l$ y sobre ella marque el segmento $\overline{QP}$, tal que $QP=a$.
- Trace la recta $k$ perpendicular a la recta $l$, en el punto $Q$.
- Sobre la recta $k$ marque el segmento $\overline{QO}$, tal que $QO=a$.
- Trace el segmento $\overline{OP}$, que es el segmento pedido.
- $OP=a\sqrt{2}$.
Propiedad
En todo triangulo rectángulo isósceles, el producto de sus tres lados es el doble del producto de sus tres alturas.
Procedimiento
- Considere el $\angle BCA$.
- Haga coincidir uno de los bordes del portasegmentos con uno de los lados del ángulo y trace una línea, como se muestra en la figura.
- Repita el mismo procedimiento, pero ahora con el otro lado del ángulo.
- Etiquete, con $P$, el punto de intersección de las dos líneas trazadas.
- Trace el rayo $\overrightarrow{CP}$, que será la bisectriz del ángulo.
Propiedad
Todos los puntos sobre la bisectriz equidistan de los lados del ángulo, $d(QM)=d(QN)$.
Procedimiento
- Trace la recta $l$ y sobre ella marque el segmento $\overline{AB}$, tal que $AB=l$.
- Trace la mediatriz del segmento $\overline{AB}$ y etiquétela $\overline{PP'}$.
- Construya el triángulo equilátero $\triangle ABO$. Para ello, solo traslade la distancia del segmento $\overline{AB}$, como se muestra en la figura.
- Prolongue los lados del triángulo y marque sobre ellos los segmentos $\overline{OE}$ y $\overline{OD}$, de longitud $l$.
- Trace la bisectriz de los ángulos $\angle AOE$ y $\angle BOD$.
- Trace, sobre las bisectrices, los segmentos $\overline{OF}$ y $\overline{OC}$, de longitud $l$.
- Trace los segmentos $\overline{EF}$, $\overline{FA}$, $\overline{BC}$, $\overline{CD}$ y $\overline{DE}$.
- El polígono $\square ABCDEF$ es el hexágono regular.
Propiedad
Se puede teselar el plano con hexágonos regulares congruentes, sin dejar ningún hueco. También, se puede hacer con los cuadrados y los triángulos equiláteros.
Procedimiento
- Considere el cuadrilátero $\square ABCD$, el rombo cuyas diagonales son $\overline{AC}$ y $\overline{BD}$, que se intersecan en el punto $O$.
- Trace las bisectrices de los ·ngulos $\angle AOD$ y $\angle COD$.
- Etiquete, con los puntos $H$ e $I$, las intersecciones de las bisectrices trazadas con los lados del rombo.
- Prolongue los segmentos $\overline{OI}$ y $\overline{OK}$ hasta que intersequen a los otros lados del rombo, en los puntos $K$ y $J$.
Propiedad
El punto de intersección $O$ de las diagonales, es el incentro del rombo.
Procedimiento
- Trace una circunferencia de centro $O$ y un diámetro $\overline{AB}$.
- Trace la mediatriz del segmento $\overline{AO}$ y etiquete con $M$ el punto donde la mediatriz interseca al radio.
- Etiquete, con $P$ y $Q$, los puntos donde la mediatriz interseca a la circunferencia.
- Tome, con el portasegmentos, la medida del segmento $\overline{PM}$.
- Trace siete cuerdas consecutivas en la circunferencia, tomando, como punto de partida, cualquiera de los extremos del diámetro y construya, en forma aproximada, el heptágono regular.
Propiedad
El heptágono es el polígono regular más pequeño, que no se puede construir con regla y compás.
Procedimiento
- Considere el cuadrilátero $\square ABCD$ un rectángulo.
- Prolongue el lado $\overline{DC}$ y sobre él marque el segmento $\overline{CE}$, tal que $\overline{CE}\cong \overline{CB}$
- Determine el punto medio $M$ del segmento $\overline{DE}$, para ello haga uso de la construcción de la mediatriz de un segmento.
- Con centro en $M$ y radio $ME$, trace un arco de circunferencia que interseque al segmento ${\overline{BC}}$, en el punto $P$.
- Construya, con el portasegmentos, el cuadrilátero $\square CPQN$ que será el cuadrado equivalente al rectángulo dado.
Propiedad
Dos o más polígonos son equivalentes si tienen la misma área.
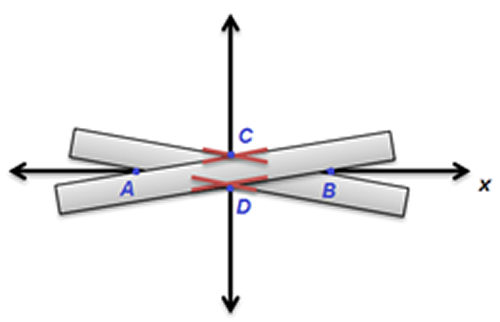 Fig. 26 Mediatriz, dado un segmento
Fig. 26 Mediatriz, dado un segmento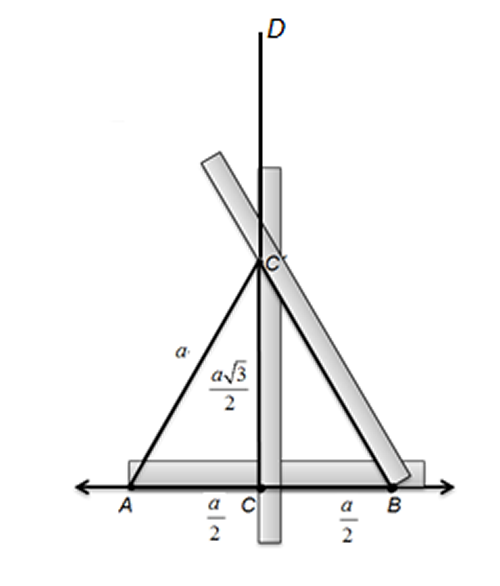 Fig. 27 Dado un segmento de longitud $a$, construir otro de longitud $a\sqrt{3}$
Fig. 27 Dado un segmento de longitud $a$, construir otro de longitud $a\sqrt{3}$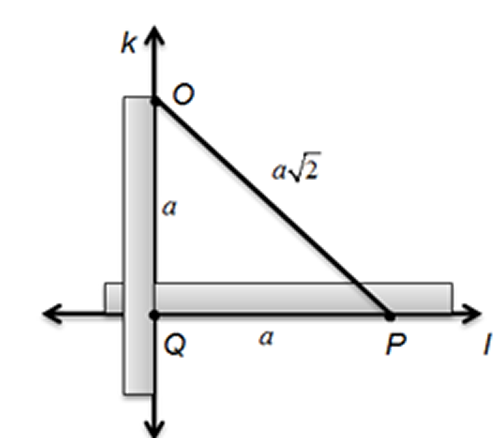 Fig. 28 Dado un segmento de longitud $a$, construir otro de longitud $a\sqrt{2}$
Fig. 28 Dado un segmento de longitud $a$, construir otro de longitud $a\sqrt{2}$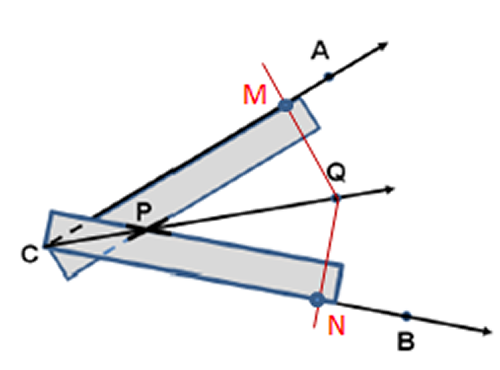 Fig. 29 Bisectriz de un ángulo
Fig. 29 Bisectriz de un ángulo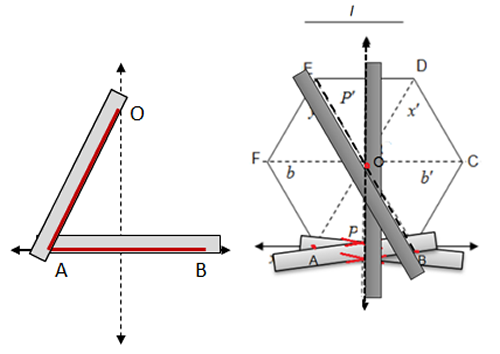 Fig. 30 Triángulo isósceles, dada la altura
Fig. 30 Triángulo isósceles, dada la altura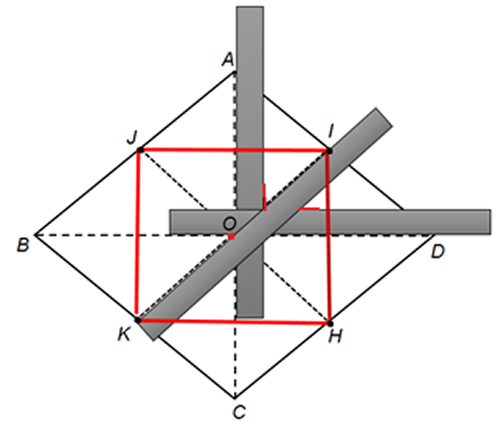 Fig. 31 Inscribir, en un rombo dado, un cuadrado cuyos lados sean paralelos a las diagonales del rombo
Fig. 31 Inscribir, en un rombo dado, un cuadrado cuyos lados sean paralelos a las diagonales del rombo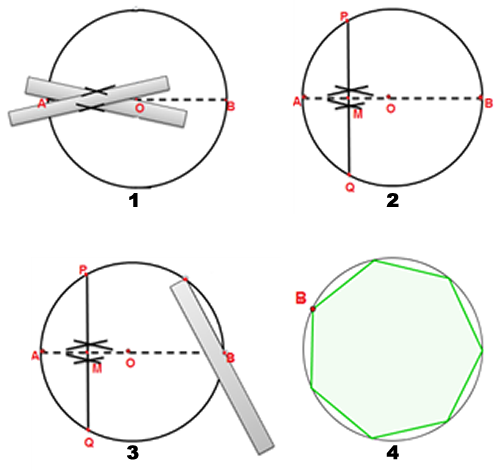 Fig. 32 Construcción aproximada de un heptágono regular
Fig. 32 Construcción aproximada de un heptágono regular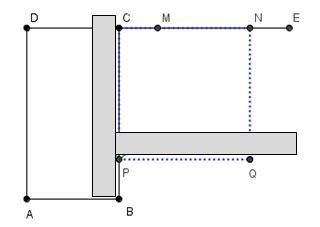 Fig. 33 Dado un rectángulo $\square ABCD$, construir un cuadrado equivalente
Fig. 33 Dado un rectángulo $\square ABCD$, construir un cuadrado equivalente