Regla y compás
Construcciones
Los dibujos geométricos que son nítidos y claros, que han sido construidos con una buena precisión, utilizando la regla y el compás; por lo general, son agradables al ojo del espectador. Es importante que el profesional en la enseñanza de la Matemática utilice la regla y el compás, en cualquier construcción geométrica realizada para sus alumnos, ya sea en la pizarra o en el papel, con el objetivo de ir perfeccionando su habilidad en el uso de estos instrumentos. Las construcciones geométricas presentadas a continuación, son muy sencillas, pero de uso común en otras construcciones más elaboradas. Tome su regla y su compás y haga las construcciones mostradas en este multimedia. ¡Anímese!
Procedimiento
- Trace una recta $\overline{y}$.
- Sobre $\overline{y}$ marque los puntos $A$ y $B$, para determinar el $\overline{AB}$.
- Con centro en $A$, trace una circunferencia de radio superior a la mitad de $\overline{AB}$.
- Con centro en $B$, trace otra circunferencia de igual radio que la anterior.
- Llame, con $C$ y $D$, a los puntos de intersección de las dos circunferencias.
- Trace la recta $\overleftrightarrow{CD}$, la cual es la mediatriz del segmento $\overline{AB}$.
Propiedad
Todos los puntos de la mediatriz de un segmento equidistan de los extremos del segmento.
Procedimiento
- Dado un $\angle Y$, trace un arco de circunferencia, con centro en el vértice del ángulo y llame, con $X$ y $Z$, a los puntos donde el arco de circunferencia interseca a los lados del ángulo.
- Trace un rayo $\overrightarrow{m}$, haga centro en $A$ y trace otro arco de circunferencia, con el mismo radio del arco anterior.
- Llame, con $B$, al punto donde el arco de circunferencia interseca al rayo $\overrightarrow{m}$.
- Marque con el compás la medida de $\overline{XZ}$.
- Con centro en $B$, trace un arco de circunferencia de radio igual a la medida de $\overline{XZ}$, llame con $C$ al punto de intersección de los dos arcos.
- Trace el rayo $\overline{AC}$ para formar el $\angle BAC$. Observe que $\angle BAC\cong \angle XYZ$.
Propiedad
Por el postulado de construcción de ángulos y dado un semiplano y un rayo, en este caso $\overline{m}$, garantiza que para cada número real entre $0^{\circ}$ y $180^{\circ}$ hay un rayo $\overrightarrow{AC}$ con $C$, que pertenece a ese mismo semiplano tal que $m\angle BAC=m\angle XYZ$, $\therefore\angle BAC\cong\angle XYZ$.
Procedimiento
- Sea la recta $\overleftrightarrow{AB}$ y un punto $P$ exterior a ella.
- Trace por $P$ una recta $\overleftrightarrow{PQ}$, donde $Q$ es el punto de intersección de dicha recta con la recta $\overline{AB}$.
- Observe que se tiene el $\angle PQA$, construya el $\angle SPQ$ (ver "Ángulo congruente, a un ángulo dado").
- Los $\angle PQA$ y $\angle SPQ$ son alternos internos congruentes, por lo tanto determinan rectas paralelas.
- Trace la recta que pasa por los puntos $P$ y $S$, tal que $\overleftrightarrow{PS}||\overleftrightarrow{AB}$.
Propiedad
Dos rectas son paralelas si son coplanares y no tienen ningún punto común. Euclides afirmó que por cualquier punto exterior a una recta, solamente puede trazarse una única recta paralela a ella. Lo anterior se conoce como el V postulado de Euclides. Precisamente, el probar la unicidad de dicha recta es lo que dió origen a las geometrías no euclideanas.
Procedimiento
- Sea el $\angle A$, que se desea bisecar.
- Con centro en $A$, trace un arco de circunferencia de radio $r$, que interseque a los lados del ángulo, en los puntos $P$ y $Q$, respectivamente.
- Trace el segmento $\overline{PQ}$ y determine su punto medio $R$ (ver construcción de la "Mediatriz, dado un segmento").
- Trace el rayo $\overrightarrow{AR}$, este rayo es la bisectriz del $\angle A$.
Propiedad
Cualquier punto de la bisectriz equidista de los lados del ángulo. Por el postulado de la adición de ángulos, se cumple que $m\angle PAQ=m\angle PAR+m\angle QAR$.
Procedimiento
- Trace el segmento $\overline{AB}$.
- Trace la mediatriz del segmento $\overline{AB}$ (ver "Mediatriz, dado un segmento").
- Sea $H$, el punto de intersecci\'{o}n de la mediatriz con $\overline{AB}$.
- Con el compás traslade la medida del segmento $\overline{GH}$, de longitud igual a la altura dada.
- Trace los segmentos $\overline{AG}$ y $\overline{BG}$.
- Como el punto $G$ pertenece a la mediatriz del segmento $\overline{AB}$, se garantiza que $\overline{AG}\cong \overline{BG}$, $\therefore\triangle AGB$ es isósceles.
Propiedad
En todo triángulo isósceles los ángulos de la base son congruentes y todas las rectas notables, trazadas desde el vértice opuesto al lado desigual, coinciden.
Procedimiento
- Trace el segmento $\overline{AB}$, de medida $h$ correspondiente a la base del triángulo equilátero.
- Con centro en $A$, trace una circunferencia que tenga por radio la medida de $\overline{AB}$.
- Con centro en $B$, trace otra circunferencia con el mismo radio del arco anterior.
- Llame, con $C$, a un punto de intersección de las dos circunferencias.
- Trace los segmentos $\overline{AC}$ y $\overline{BC}$, respectivamente.
- El $\triangle ABC$ es equilátero.
Propiedad
En el triángulo equilátero todas las rectas notables coinciden. El área de un triángulo equilátero viene dada por la fórmula $A=\frac{L^{2}\sqrt{3}}{4}$, donde $L$ es la medida del lado del trángulo.
Procedimiento
- Trace el segmento $\overline{AB}$, correspondiente a uno de los lados del cuadrado.
- Trace una perpendicular que pase por el punto $A$ y otra por el punto $B$ (ver "Mediatriz, dado un segmento" y "Paralela, a una recta dada").
- Trace una circunferencia con centro en $A$ y que tenga por radio la medida de $\overline{AB}$.
- Trace una circunferencia con centro en $B$ y que tenga por radio la medida de $\overline{AB}$.
- Llame, con $P$ y $Q$, a los puntos de intersección de cada circunferencia con las perpendiculares trazadas.
- Trace el segmento $\overline{PQ}$.
- El cuadrilátero $\square APQB$ es un cuadrado.
Propiedad
El cuadrado es un cuadrilátero equiángulo. Sus diagonales se bisecan perpendicularmente y determinan cuatro triángulos congruentes.
Procedimiento
- Trace el segmento $\overline{AB}$.
- Trace una perpendicular en cada extremo de $\overline{AB}$ (ver "Cuadrado, dado un lado").
- Trace una circunferencia con centro en $A$ y que tenga por radio la medida de $\overline{AB}$.
- Trace una circunferencia con centro en $B$ y que tenga por radio la medida de $\overline{AB}$.
- Llame, con $P$ y $Q$, a los puntos de intersección de cada circunferencia, con las perpendiculares trazadas.
- Trace el segmento $\overline{PQ}$.
- El cuadrilátero $\square APQB$ es un cuadrado.
- Trace el punto medio $M$ de $\overline{AB}$ (ver "Mediatriz, dado un segmento").
- Trace una circunferencia con centro en $M$ y que tenga por radio la medida de $\overline{MQ}$.
- Prolongue el segmento $\overline{AB}$, de tal forma que interseque a la circunferencia en un punto $C$.
- Trace una perpendicular que pase por el punto $C$ (ver "Cuadrado, dado un lado").
- Con el compás, traslade la medida del segmento $\overline{CR}$, de longitud igual a la medida del lado del cuadrado $\square APQB$.
- Trace el segmento $\overline{PR}$.
- El cuadrilátero $\square APRC$ es un rectángulo áureo.
Propiedad
Los lados del rectángulo áureo están en una proporción, igual a la razón áurea: $\frac{a+b}{a}=\frac{a}{b}$, $\Phi=\frac{1+\sqrt{5}}{2}$.
Procedimiento
- Trace el segmento $\overline{AB}$, correspondiente a uno de los lados del pentágono.
- Trace el punto medio $M$ de $\overline{AB}$ (ver "Mediatriz, dado un segmento").
- Prolongue el segmento $\overline{AB}$.
- Trace una perpendicular que pase por $M$ y otra que pase por $B$ respectivamente (ver "Cuadrado, dado un lado").
- Con centro en $B$, trace un arco de circunferencia de radio igual a la medida de $\overline{AB}$, de tal manera que interseque a la perpendicular trazada por $B$ en el punto $R$.
- Con centro en $M$, trace un arco de circunferencia de radio igual a la medida de $\overline{MR}$, de tal manera que interseque a la prolongación del segmento $\overline{AB}$ en el punto $S$.
- Con centro en $A$, trace un arco de circunferencia de radio igual a la medida de $\overline{AS}$, de tal manera que interseque a la perpendicular trazada por $M$ en el punto $D$.
- Con centro en los puntos $A$, $B$ y $D$; trace arcos de circunferencia de radio igual a la medida del segmento $\overline{AB}$.
- Llame, con los puntos $C$ y $E$, a las intersecciones de los arcos.
- Trace los segmentos $\overline{AE}$, $\overline{ED}$, $\overline{DC}$ y $\overline{CB}$.
- El polígono $AEDCB$ es un pentágono regular.
Propiedad
En un pentágono regular, la diagonal y el lado están en la proporción áurea, esto es $\Phi=\frac{1+\sqrt{5}}{2}$.
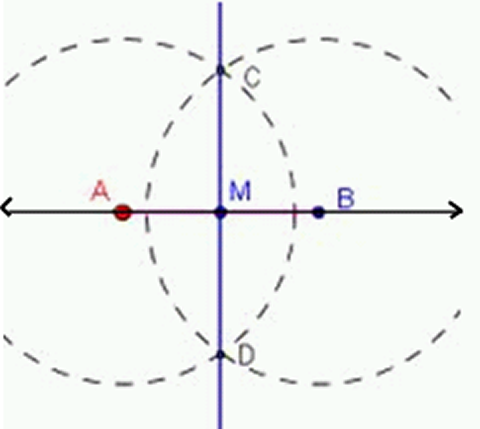 Fig. 6 Mediatriz, dado un segmento
Fig. 6 Mediatriz, dado un segmento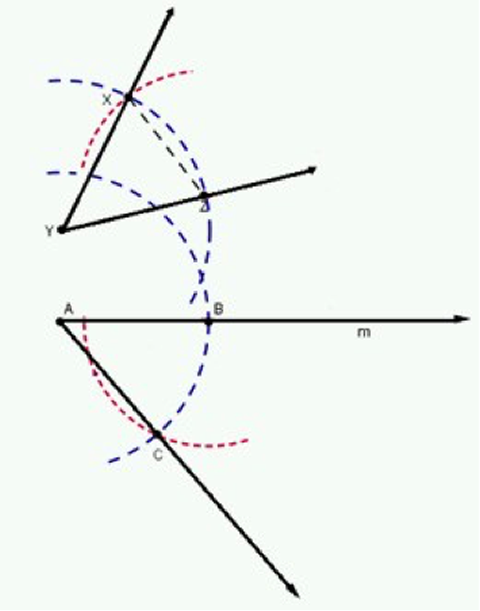 Fig. 7 Ángulo congruente, a un ángulo dado
Fig. 7 Ángulo congruente, a un ángulo dado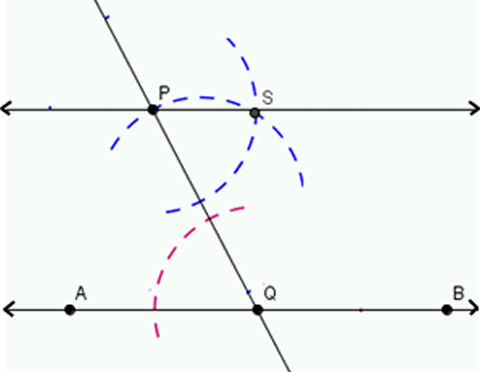 Fig. 8 Paralela, a una recta dada
Fig. 8 Paralela, a una recta dada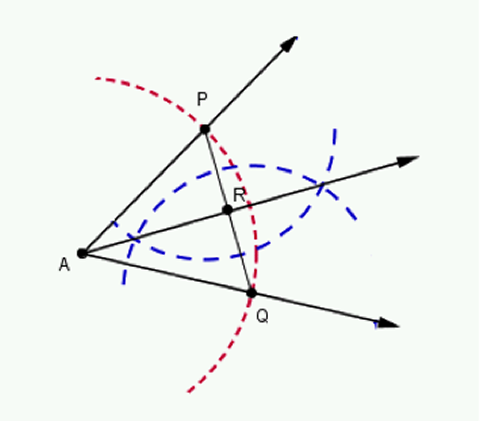 Fig. 9 Bisectriz de un ángulo
Fig. 9 Bisectriz de un ángulo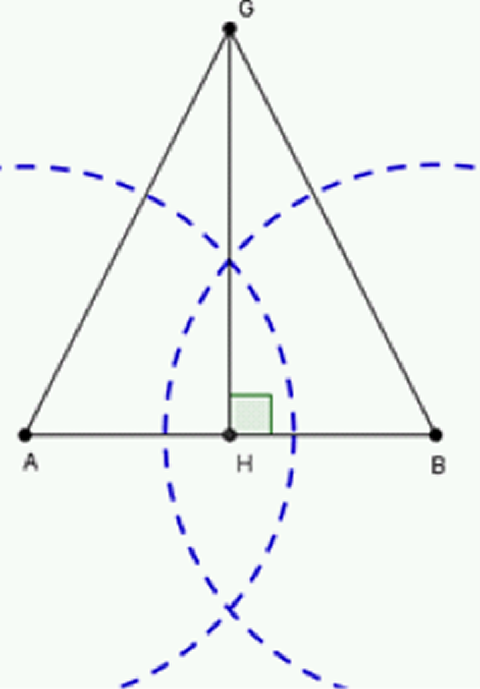 Fig. 10 Triángulo isósceles, dada la altura
Fig. 10 Triángulo isósceles, dada la altura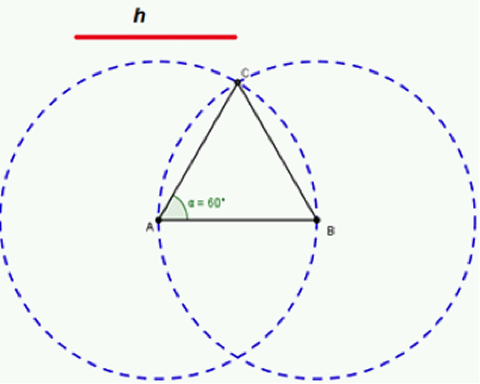 Fig. 11 Triángulo equilátero, dado un lado
Fig. 11 Triángulo equilátero, dado un lado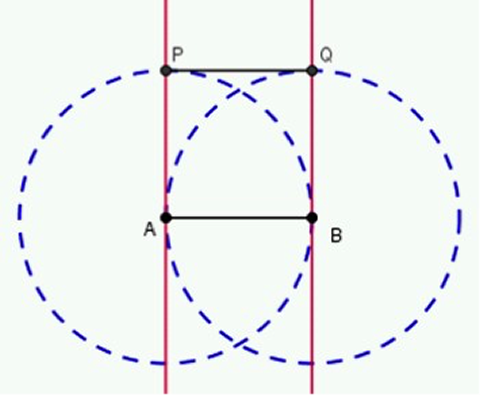 Fig. 12 Cuadrado, dado un de sus lados
Fig. 12 Cuadrado, dado un de sus lados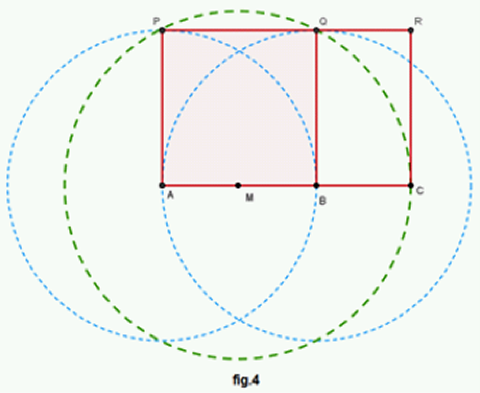 Fig. 13 El rectángulo áureo
Fig. 13 El rectángulo áureo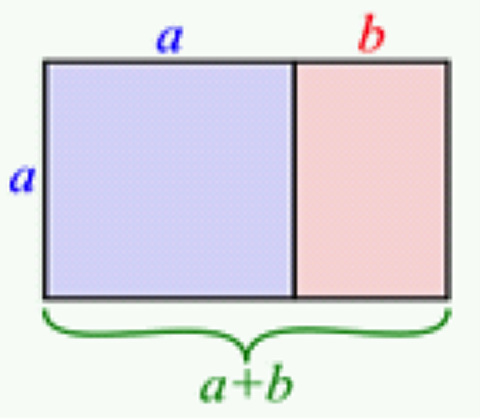 Fig. 14 El rectángulo áureo
Fig. 14 El rectángulo áureo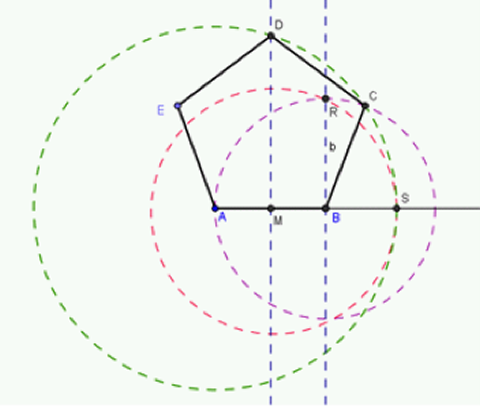 Fig. 15 Pentágono regular
Fig. 15 Pentágono regular