Doblado de papel
Construcciones
Con el doblado de papel también se pueden lograr construcciones geométricas nítidas y claras, de la misma forma que cuando se utiliza la regla, el compás y el portasegmentos, solamente se necesita precisión y cierto grado de habilidad.
Las construcciones geométricas, que se presentan a continuación, son muy sencillas y algunas de ellas ya fueron construidas con la regla, el compás y el portasegmentos (ver construcciones geométricas con “Regla y compás” y con “Portasegmentos”).
Para realizar las construcciones, siga las siguientes recomendaciones:
- Todos los dobleces y pliegues deben hacerse con exactitud.
- Trabajar sobre una superficie lisa y sólida.
- Repase los dobleces y pliegues con la uña del dedo pulgar, estos se marcarán mejor.
- No se debe omitir ningún paso.
Procedimiento
- Trace el segmento $\overline{AB}$.
- Doble la hoja, de forma que haga coincidir el punto $A$ con el punto de $B$.
- Desdoble la hoja y trace una recta por el pliegue obtenido anteriormente, el cual es la mediatriz del segmento.
Propiedad
Todos los puntos de la mediatriz de un segmento equidistan de los extremos de dicho segmento.
Procedimiento
- Considere el $\triangle ABC$ con $BD=h$, $h$ altura sobre el lado $\overline{AC}$ y $AC=b$.
- Haga coincidir el vértice $B$ con el punto $D$, como se muestra en 2 de la figura 54.
- Haga coincidir los vértices $A$ y $C$ con el vértice $D$, como se muestra en 3 de la figura 54. Note que se forma un rectángulo, cuyo ancho es $\frac{h}{2}$ y su largo es $\frac{b}{2}$.
- $A_{\mbox{rectángulo}}=(\frac{1}{2}b)(\frac{1}{2}h)=\frac{1}{4}b h$.
- El área del triángulo es el doble del área del rectángulo.
- $A_{\mbox{triángulo}}=2\cdot (\frac{1}{4}b\cdot h)=\frac{bh}{2}$.
Propiedad
El área del $\triangle ABC$ también se puede calcular con la fórmula a$\triangle ABC=\frac{(AC)(AB) \sin A}{2}$.
Procedimiento
- Tome una hoja rectangular, dóblela por la mitad, paralelamente a los lados mayores.
- Con un doblez que pase por el punto $B$, lleve el punto $A$ sobre la paralela media, específicamente hasta $A'$, tal que se forme el $\angle CBD$ cuya medida es igual a $60^{\circ}$.
- Sin desdoblar la figura anterior, trace la bisectriz del $\angle CBD$, haga coincidir los lados $\overline{BC}$ y $\overline{BD}$.
- $\angle CBA'\cong DBA'$, la medida de estos ángulos es igual a $30^{\circ}$.
- Repita el procedimiento con un ángulo de $30^{\circ}$ para obtener un ángulo de $15^{\circ}$.
Propiedad
En un triángulo, la razón entre dos lados es igual a la razón de las partes, en las que queda dividido el tercer lado por la bisectriz de ángulo interno opuesto.
Procedimiento
- Trace la recta $\overleftrightarrow{AB}$.
- Marque un punto $P$, exterior a $\overleftrightarrow{AB}$.
- Trace una recta perpendicular a $\overleftrightarrow{AB}$, que pase por el punto $P$ (ver “Mediatriz, dado un segmento”).
- Trace una recta perpendicular $\overleftrightarrow{XY}$, que pase por el punto $P$ (ver “Mediatriz, dado un segmento”).
- $\overleftrightarrow{AB} \parallel \overleftrightarrow{XY}$
Propiedad
Dos rectas perpendiculares a una tercera son paralalelas, esto es: si $\overleftrightarrow{AB} \perp \overleftrightarrow{l}\wedge \overleftrightarrow{XY} \perp \overleftrightarrow{l}$, entonces $\overleftrightarrow{AB} \parallel \overleftrightarrow{XY}$.
Procedimiento
“Los tres puntos de intersección de las rectas adyacentes que trisecan los tres ángulos de un $\triangle ABC$ determinan un triángulo equilátero”.
- Construya un $\triangle ABC$.
- Trace las trisectrices de cada ángulo. Haga un doblez hacia adelante (sin marcar todavía), que pase por el punto $A$, y de forma que se vea aproximadamente igual al ángulo doblado y el que resta de $A$. Sujete con el dedo el doblez (sin marcar todavía), doble hacia atrás el ángulo restante, de forma que se vea un ángulo triple en $A$, el cual debe ajustar hasta que coincidan sus lados, cuando lo consiga marque los dobleces.
- Repita el proceso con los vértices $B$ y $C$, para que obtenga el triángulo con sus trisectrices marcadas.
- Marque la intersección de dos trisectrices, el triángulo formado en el interior del triángulo mayor es equilátero.
Propiedad
Los puntos de intersección de los trisectores de los ángulos, de cualquier $\triangle ABC$, determinan triángulos equiláteros.
Procedimiento
- Dibuje, en una hoja de papel, un círculo de radio $r$ y centro $O$. Luego, recórtelo, como se muestra en la figura.
- Marque en el interior del círculo un punto $P$ y varios en la circunferencia como se muestra en la figura.
- Haga coincidir cada punto que marcó en la circunferencia, con el punto $P$, de manera que por dichos puntos exista un único doblez.
- Los dobleces irán delimitando el contorno de la elipse, como se muestra en la figura.
Propiedad
La ecuación de una elipse, centrada en el punto $(h,k)$, viene dada por la fórmula $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$.
Procedimiento
- Tome una hoja de papel cuadrada, trace dos ejes de simetría y doble, nuevamente, por la mitad como se muestra en la figura 63.
- Marque los puntos $A$ y $B$ y haga coincidir el punto $A$ sobre el eje de simetría, determinando el punto $C$. Se forma de esta manera el $\triangle ABC$, recto en $C$, como se muestra en la figura 64.
- Repita el paso anterior, para los otros tres vértices del cuadrado.
- Desdoble el papel a su forma original y denomine los lados del cuadrado, como se muestra en la figura 65.
- Observe que se tiene un cuadrado de lado $a+b$, otro de lado $c$ y cuatro triángulos rectángulos de catetos $a$ y $b$, respectivamente.
- Se tiene que probar que $a^2+b^2=c^2$.
- El área del cuadrado de lado $a+b$, es igual al área de los cuatro triángulos rectángulos más el área del cuadrado de lado $c$.
- $(a+b)^2=4\cdot(\frac{ab}{2})+c^2$, por suma de áreas.
- $a^2+2ab+b^2=2ab+c^2$, por la primera fórmula notable.
- $a^2+\cancel{2ab}+b^2=\cancel{2ab}+c^2$, por suma de opuestos.
- $a^2+b^2=c^2$.
Propiedad
Terna pitagórica de Mesopotamia $(2mn, \;m^2-n^2,\; m^2+n^2)$, con $m>n$
Terna pitagórica de Pitágoras $(2n+1,\; 2n^2+2n, \;2n^2+2n+1)$, con $n\neq 0$
Terna pitagórica de Platón $(2n, \;n^2-1, \;n^2+1)$, con $n>1$
Procedimiento
- Tome una hoja de papel y forme el cuadrado $\square ABCD$.
- Trace los puntos medios $E$, $F$, $G$, $H$, de cada uno de los lados del cuadrado. (ver construcción “Mediatriz, dado un segmento”).
- Doble el papel por los puntos $E$ y $F$ y marque el segmento $\overline{EF}$, haga lo mismo con los otros puntos y marque los segmentos $\overline{FG}$, $\overline{GH}$, $\overline{FH}$ para obtener el cuadrado $\square EFGH$, inscrito en el cuadrado $\square ABCD$.
- Haga coincidir los segmentos $\overline{EB}$ y $\overline{EF}$, para obtener la bisectriz del $\angle BEF$.
- Haga coincidir los segmentos $\overline{FB}$ y $\overline{FE}$, para obtener la bisectriz del $\angle BFE$.
- Denomine el punto de intersección de las dos bisectrices con la letra $J$.
- Repita el procedimiento anterior para los vértices $A$, $C$ y $D$.
- El polígono $EJFKGLHI$, es el octógono regular.
Propiedad
Un octógono tienen 20 diagonales y la suma de sus ángulos internos es igual a $1080^{\circ}$.
Procedimiento
- Tome una hoja de papel rectangular para construir un triángulo equilátero (ver construcción “Ángulos de $15^{\circ}$, $30^{\circ}$ y $60^{\circ}$”).
- Trace las mediatrices de los lados del triángulo (ver construcción “Mediatriz, dado un segmento”).
- Etiquete el punto de intersección de las tres mediatrices (circuncentro), con la letra $O$.
- Haga coincidir los vértices del triángulo con el punto $O$, para formar el hexágono regular.
Propiedad
Con hexágonos regulares congruentes se puede teselar el plano. Los cuadrados y los triángulos equiláteros son los otros polígonos que verifican esta propiedad.
Procedimiento
- Tome una hoja de papel rectangular para construir un triángulo equilátero (ver construcción “Ángulos de $15^{\circ}$, $30^{\circ}$ y $60^{\circ}$”).
- Trace las bisectrices de los ángulos del triángulo, como se muestra en la figura 68.
- Marque el punto de intersección de las bisectrices (incentro).
- Haga coincidir un vértice del triángulo con el punto de intersección de la bisectriz del lado opuesto, como se muestra en la figura 69.
- Repita el paso anterior para los otros dos vértices del triángulo, obsérvese la figura 70.
- Doble cada triángulo por su altura, de manera que el doblez contenga al incentro del triángulo como se muestra en la figura 71.
- Luego de realizado el procedimiento anterior, obtiene la estrella de seis picos, como se muestra en la figura 72.
- Dar la vuelta a la estrella por la cara lisa, observe la figura 73.
Propiedad
La estrella de seis picos está formada por dos triángulos equiláteros, todos sus vértices están conectados y puede dibujarse sin “levantar” el lápiz del papel.
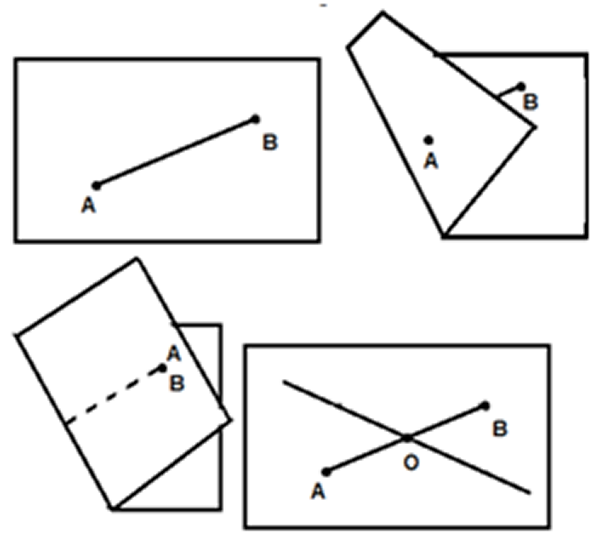 Fig. 53 Mediatriz, dado un segmento
Fig. 53 Mediatriz, dado un segmento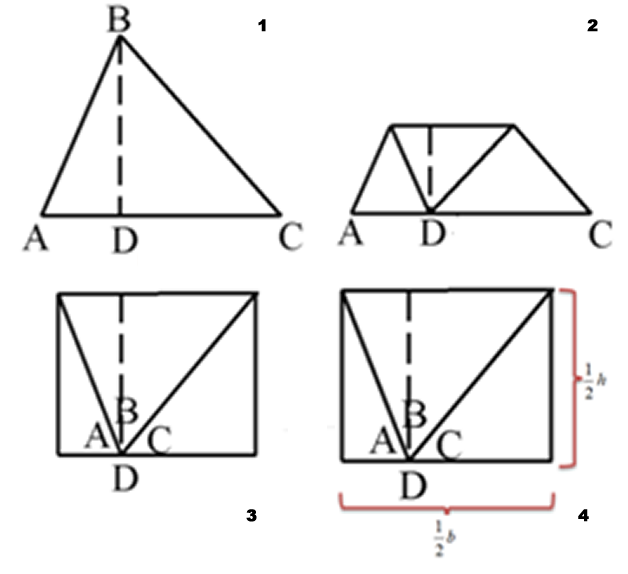 Fig. 54 Área del triángulo
Fig. 54 Área del triángulo Fig. 55 Ángulos de $15^{\circ}$, $30^{\circ}$ y $60^{\circ}$
Fig. 55 Ángulos de $15^{\circ}$, $30^{\circ}$ y $60^{\circ}$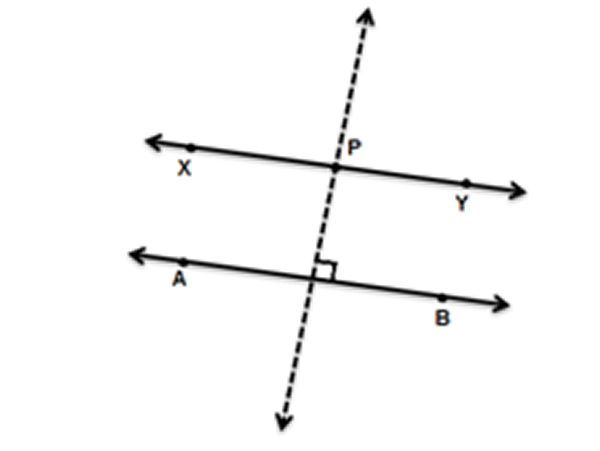 Fig. 56 Dado un punto exterior a una recta, trazar una recta paralela por dicho punto
Fig. 56 Dado un punto exterior a una recta, trazar una recta paralela por dicho punto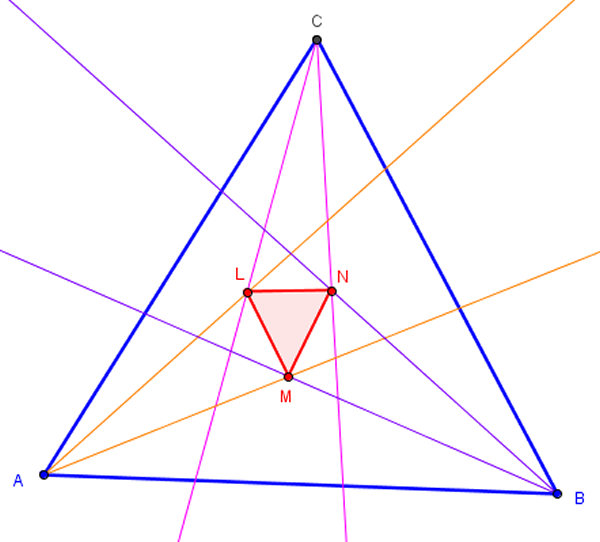 Fig. 57 Teorema de Morley
Fig. 57 Teorema de Morley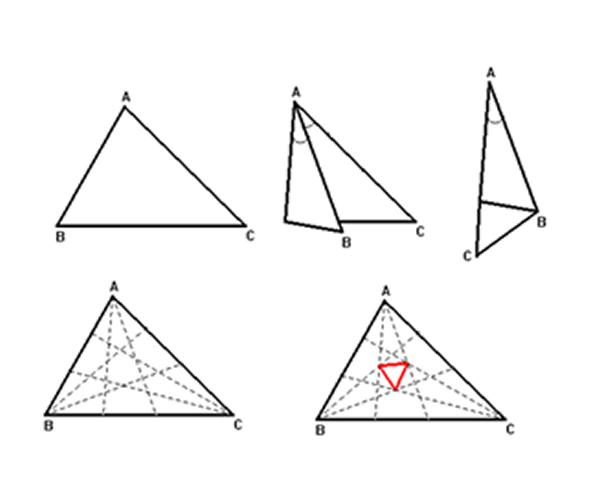 Fig. 58 Doblado del triángulo
Fig. 58 Doblado del triángulo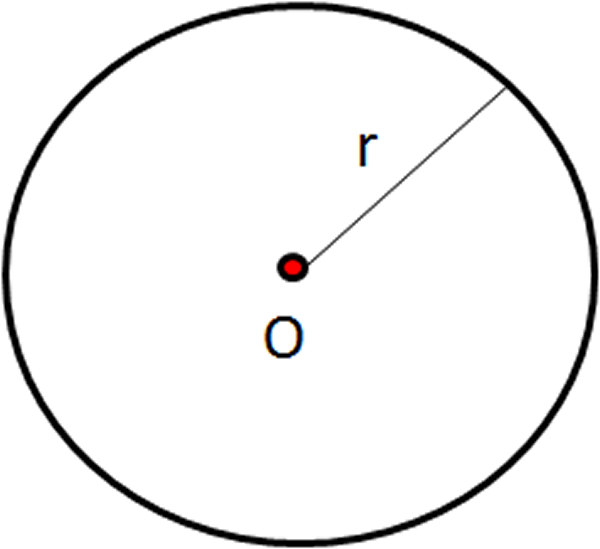 Fig. 59 Círculo de radio $r$
Fig. 59 Círculo de radio $r$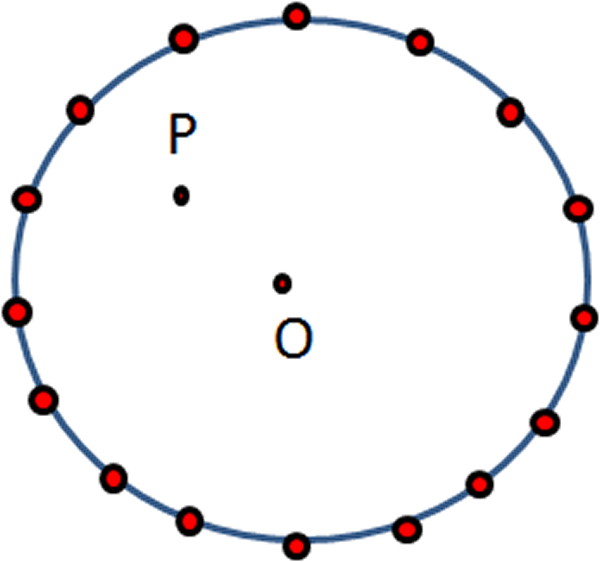 Fig. 60 Punto $P$ y varios en la circunferencia
Fig. 60 Punto $P$ y varios en la circunferencia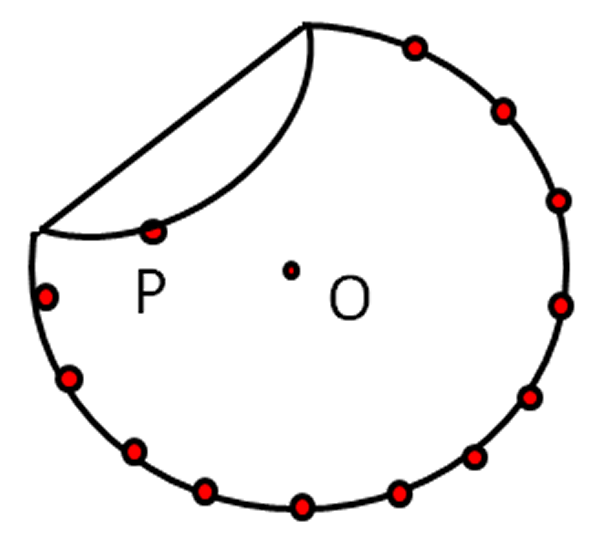 Fig. 61 Doblado del papel
Fig. 61 Doblado del papel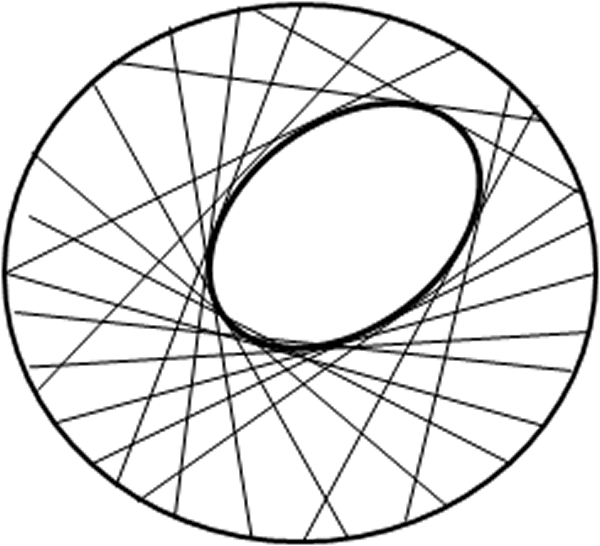 Fig. 62 Los dobleces delimitaron el contorno de la elipse
Fig. 62 Los dobleces delimitaron el contorno de la elipse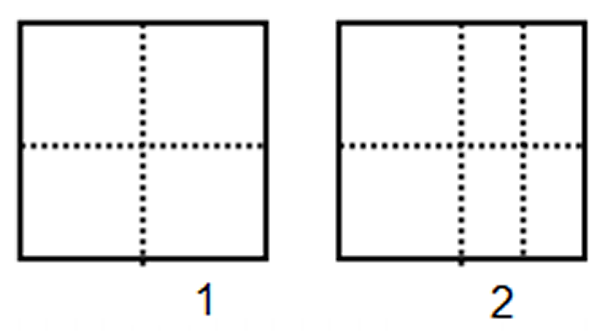 Fig. 63 Ejes de simetría
Fig. 63 Ejes de simetría Fig. 64 Doblado del papel
Fig. 64 Doblado del papel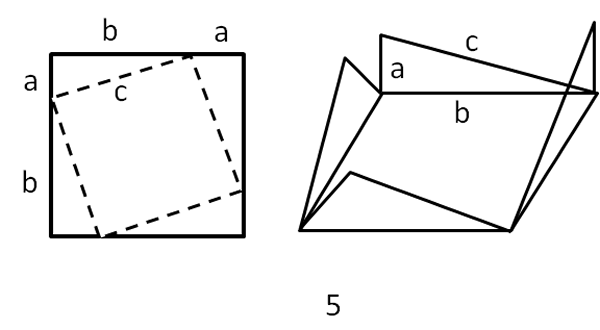 Fig. 65 Desdoblado del papel
Fig. 65 Desdoblado del papel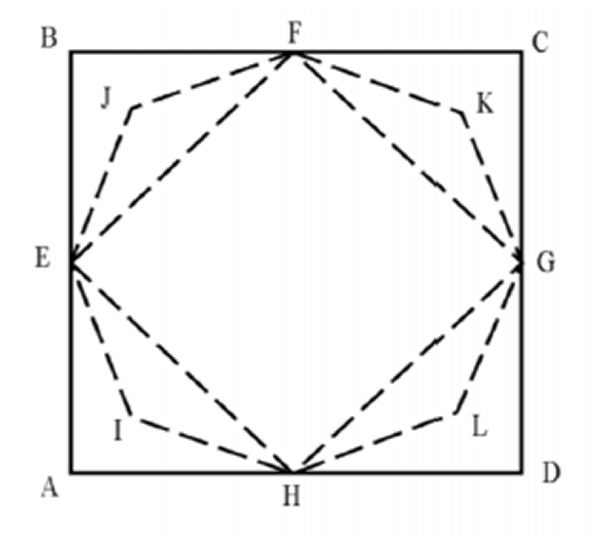 Fig. 66 Octógono regular
Fig. 66 Octógono regular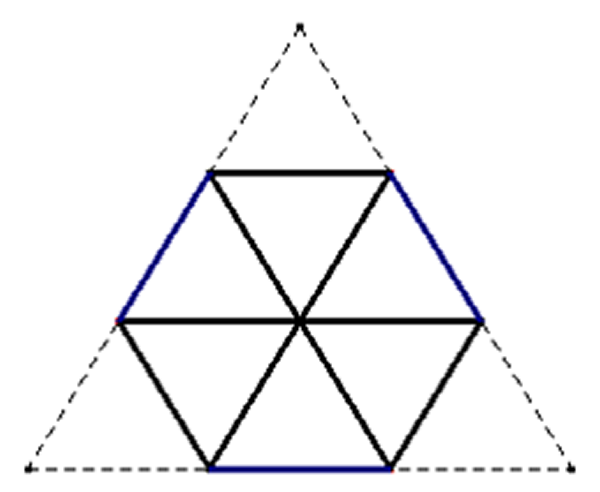 Fig. 67 Hexágono regular
Fig. 67 Hexágono regular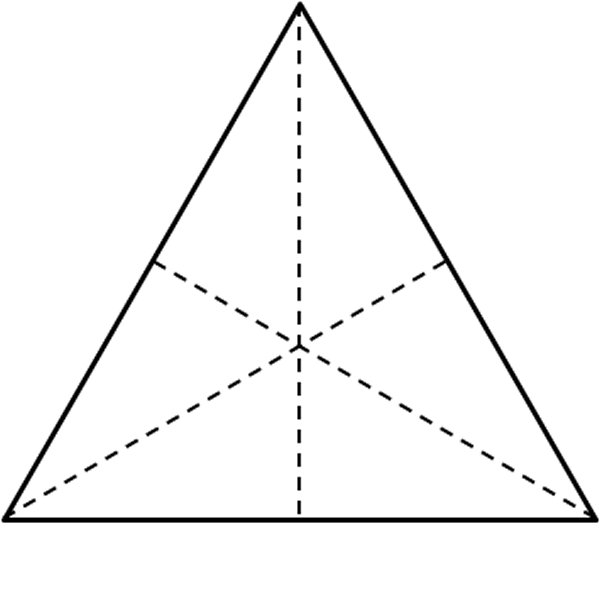 Fig. 68 Bisectrices del triángulo
Fig. 68 Bisectrices del triángulo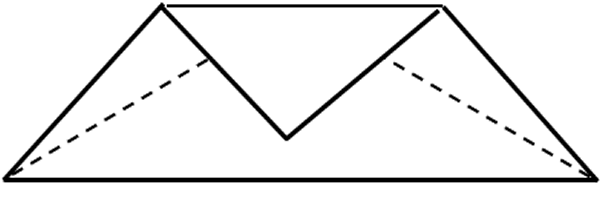 Fig. 69 Doblado en las bisectrices
Fig. 69 Doblado en las bisectrices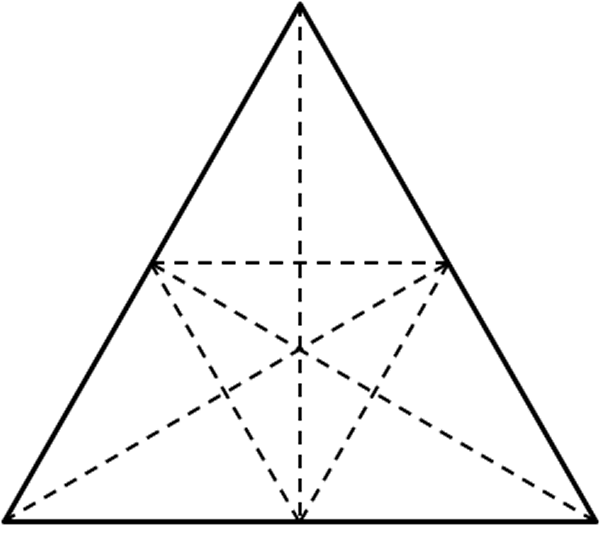 Fig. 70 Doblado en los tres vértices
Fig. 70 Doblado en los tres vértices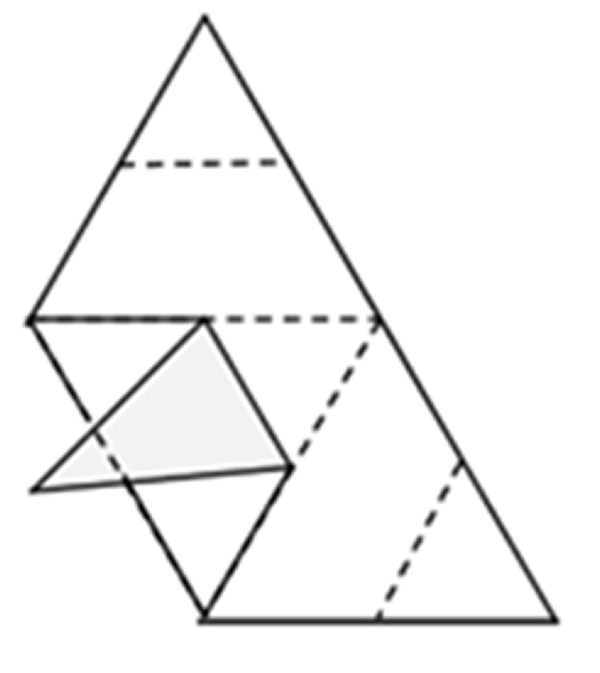 Fig. 71 Doblado por la altura
Fig. 71 Doblado por la altura Fig. 72 Estrella de seis picos
Fig. 72 Estrella de seis picos Fig. 73 Reverso de la estrella
Fig. 73 Reverso de la estrella