Matemática moderna
Antes de la década de 1950, el curriculum en matemática de secundaria no utilizaba conceptos o ejercicios que incluyeran las teorías conjuntistas desarrolladas durante el siglo XX. Tampoco había restricciones para las variables cuando se enunciaban propiedades pues, para la época, los programas de estudio no contemplaban dichos conocimientos.
En Álgebra se daba énfasis a lo rutinario y mecánico, y se le dedicaba mucho tiempo a la resolución de una cantidad desmedida de ejercicios. En Aritmética, se trabajaba la numeración y las operaciones con enteros y fracciones como se hace hoy. Además, se estudiaba el sistema monetario y el sistema métrico decimal. Dado que no existían las calculadoras o computadoras para apoyar el trabajo, se dedicaban en los libros de texto capítulos completos con tablas para indicar, por ejemplo, los logaritmos y las funciones trigonométricas y en la lecciones se dedicaba mucho tiempo en explicar a los y las estudiantes cómo utilizar dichas tablas.
Ejemplo 1. Ejercicio de cálculo mental muy utilizado a inicios de la década de 1950.
Sume y reste
Cálculo oral:
| 1. | 45 + 25 | 19 + 11 | 36 + 15 | 36 + 12 |
| 98 + 13 | 13 + 08 | 23 + 10 | 48 + 36 | |
| 51 + 17 | 92 + 56 | 98 + 74 | 44 + 17 | |
| 36 + 11 | 45 + 36 | 65 + 95 | 85 + 23 | |
| 92 + 42 | 96 + 85 | 19 + 27 | 11 + 15 |
| 2. | 15 + 12 | 44 + 51 | 56+ 15 | 91 + 39 |
| 93 + 35 | 36 + 12 | 39 + 85 | 36 + 49 | |
| 89 + 66 | 56 + 89 | 91 + 22 | 44 + 22 | |
| 78 + 72 | 44 + 36 | 36 + 17 | 31 + 17 | |
| 93 + 33 | 56 + 45 | 95 + 75 | 18 + 92 |
Restar sucesivamente todas las veces que pueda:
- 62 – 23
- 58 – 12
- 98 – 44
- 45 – 16
- 77 – 21
Tarea:
Repita la tabla del siete diez veces.
Como se muestra en el Ejemplo 1, se privilegia el cálculo mecánico y se deja de lado la comprensión del concepto; se antepone la excesiva memorización.
A partir de la década de los sesenta, la investigación en Educación Matemática tuvo un fuerte impulso en el ámbito internacional; se crearon revistas y se celebran congresos; además, la didáctica comienzó a formar parte del programa de formación de los futuros profesores.
El lanzamiento en 1957 del Sputnik por la Unión de Repúblicas Socialistas Soviéticas (URSS) propició en Estados Unidos la sensación de inferioridad en los campos científico y tecnológico. En este contexto, surgió la idea, secundada en los ámbitos políticos y económicos, de que era necesaria una reforma en la Educación Matemática en el país del norte. Para ello, se pensó que habría que abandonar la enseñanza “tradicional”, con una Matemática con contenidos separados que databan del siglo XVI y ser sustituidas por otras supuestamente más modernas (Sorando, J; 2002, p.123). En el Congreso de Royaumont, en Francia, en 1959, bajo la consigna “Abajo Euclides”, se impulsó el inicio de la reforma. Dada la importancia de la Matemática abstracta durante el último siglo, con la unificación de sus ramas mediante conceptos generales y estructuras, se propuso reconstruir la Matemática de la enseñanza básica y secundaria desde ese punto de vista global (Sorando, J; 2002, p.123). Para intentarlo, se introdujeron algunas nociones de la Teoría de Conjuntos (conjuntos y aplicaciones) y del Álgebra abstracta (grupos, espacios vectoriales), acompañado de numerosos cambios tanto en la materia del currículo como en la forma de presentarla.
Ejemplo 2. Material utilizado durante la reforma de la matemática moderna.

Todo lo anterior causó inquietud no solamente entre los padres de los alumnos, sino también entre los y las docentes porque muchos tuvieron que aprender algo nuevo y no resultaba tan fácil. Se cambió mucho el contenido y la manera de escribir los libros de texto; se puso en circulación una terminología tan abundante como engorrosa para los estudiantes. Se dejó de lado la Geometría clásica presente en los elementos de Euclides y se pasó a la Geometría analítica que implicaba ecuaciones de rectas y curvas con apoyo del álgebra lineal. Se intentó aumentar la precisión del lenguaje matemático y el rigor de los razonamientos en detrimento de la intuición, en particular de la Geométrica.
La principal inspiración matemática de la reforma provenía de Nicolás Bourbaki, pseudónimo empleado por algunos de los mejores matemáticos franceses que desde 1935 se habían unido para emprender la empresa de publicar una serie de libros que con el título Elementos de Matemáticas. Su objetivo era ofrecer una presentación bien organizada y fundamentada de esta ciencia para lo que utilizaron como elemento unificador la noción de estructura matemática, dividida a su vez en algebraica y el lenguaje de Teoría de Conjuntos.
Este movimiento contó con la influencia del psicólogo suizo Jean Piaget, considerado el padre de la Psicología evolutiva; Piaget ofrecía una base psicológica de la estructura que proponía Bourbaki.
El objetivo inicial de este grupo de matemáticos era escribir un tratado que viniera a llenar el vacío existente en esa época en Francia en el área de análisis en el nivel de licenciatura. Sin embargo, para el segundo congreso en 1938 fue claro que el fin inicial era demasiado ambicioso por lo que se decidió reemplazarlo por el proyecto de construir una base clara para todas las teorías existentes en matemática pura. Los artículos y trabajos realizados por Bourbaki nunca fueron pensados para ser utilizados en enseñanza secundaria.
Figura 1. Grupo de matemáticos en el Primer Congreso Bourbaki en julio de 1935 (de izquierda a derecha: Simone Weil, Charles Pisot, André Weil, Jean Dieudonné, Claude Chabauty, Charles Ehresmann y Jean Delsarte).

Durante la década de los sesenta la reforma fue implementada en Europa, Norteamérica y América Latina; se escribieron libros de texto, se reformularon los programas de estudio y se dictaban conferencias del tema pero después de unos cuantos años tratando de poner a funcionar la reforma, esta tendencia finalmente fracasó.
Según los opositores de esta visión el error residía en ofrecer a los estudiantes la versión última y perfeccionada de la matemática, y no una matemática creada con intuiciones, experimentación y muchos fracasos. En la Matemática Moderna se consideraba a las Matemáticas autosuficiente olvidando que las Matemáticas existen para ayudar al hombre a comprender y dominar el mundo físico (Sorando, J; 2002, p. 125).
Uno de los principales opositores a este movimiento fue Morris Kline que en su libro Por qué Juanito no sabe sumar (1973) explicó ampliamente las razones por las cuales dicha reforma estaba destinada al fracaso, entre las que se puede citar su planteamiento de que una Matemática por sí misma y para sí misma no pueden ser atractiva para los estudiantes.
Según Ruíz, la reforma fracasó debido a las siguientes razones:
- Era correcto buscar mejorar y modernizar la enseñanza de las Matemática, pero no implicaba introducir la Matemática moderna de las universidades en los contenidos de la Matemática preuniversitaria.
- Era incorrecto presumir un curriculum para todo el mundo igual para asumir una continuación en la educación universitaria, de seguir carreras científicas y técnicas.
- Era incorrecto pensar que los matemáticos tenían las condiciones para determinar un currículo de Matemática preuniversitaria por el solo hecho de ser matemáticos profesionalmente competentes; tampoco era cierto que estuvieran dotados de la filosofía y la visión educativas más apropiadas.
- Era incorrecto porque tanto la ideología Bourbaki como todos los supuestos filosóficos de los que se nutría, eran y son dudosamente válidos.
- Se pensaba y todavía muchos piensan que la matemática es más importantes de lo que es, lo que a veces es una visión extendida en la comunidad matemática; se considera que el papel de la Matemática en la ciencia y la tecnología moderna se puede trasmitir mecánicamente a la educación: algo así como si se aprende teoría de grupos, categorías y espacios topológicos vectoriales, el hecho mismo apuntala mecánicamente “por arte de magia” la ciencia, la tecnología, y el desarrollo nacional. Eso no es cierto: el aporte de la matemática a la ciencia, y de esta a la tecnología y la sociedad depende de una colección muy densa y compleja de mediaciones teóricas y prácticas. (2006, pp. 16-17)
Situación en nuestro país
La reforma de la Matemática Moderna como tendencia mundial llegó a nuestro país a finales de la década de los sesenta y logró institucionalizarse de manera significativa en todos los niveles de educación básica y media.
Las primeras incursiones en Latinoamérica provenían de libros de texto traídos de Estados Unidos. En la primera conferencia Iberoamericana de Educación Matemática, realizada por el Comité Interamericano de Educación Matemática (CIAEM ) en el año de 1961, en Bogotá, se realizan las primeras intervenciones sobre las matemáticas modernas y su introducción en la educación secundaria. El Prof. Bernardo Alfaro Sagot asistió como representante por Costa Rica a esta conferencia; el profesor Alfaro, una vez que regresó empezó a trabajar en la reforma publicando libros de texto que incluían las ideas de la reforma.
En nuestro país los programas oficiales de Matemática para primaria y secundaria aprobados en 1964 ya incluían los cambios; Costa Rica se convirtió en el primer país latinoamericano en introducir la reforma.
Para 1966, en la segunda conferencia Iberoamericana de Educación Matemática a cargo del CIAEM, se redactó un temario que contempló toda la educación secundaria bajo las ideas de la Matemática moderna.
Otro hecho transcendental en el desarrollo de la reforma de la Matemática moderna en nuestro país fue que una vez que ocurrió la separación del Departamento de Física y Matemática en 1971 en la Universidad de Costa Rica (UCR), el primer director fue Francisco Ramírez. El Prof. Ramírez había estudiado en Francia, donde recibió una gran influencia de las ideas bourbakianas, razón por la cual promovió la incorporación de profesores franceses, así como el envío de estudiantes costarricenses a realizar estudios en ese país europeo. De lo anterior, se puede afirmar que la formación de profesores de matemática fue muy influida por la Matemática moderna. Profesores tales como: Gil Chaverri, Manuel Calvo, Guillermo Vargas o Inés Azofeifa participaron activamente publicando libros utilizados en III ciclo y Educación Diversificada que aún se pueden encontrar en bibliotecas.
La Matemática moderna como un movimiento colectivo internacional permitió en algunas naciones, como el caso de Costa Rica, dotar a los matemáticos de un lugar social y profesional propio, relevante; fortificar sus lazos internacionales y, por ello, contribuir al desarrollo de comunidades matemáticas, las cuales, en la mayoría de los casos, siempre habían tenido un lugar muy reducido en las diferentes universidades. (Ruiz, 2003)
Ejemplo 3. Material utilizado durante la reforma de las matemáticas modernas en Costa Rica.
Ecuación vectorial de una recta
Sabemos de Geometría que dos puntos: $P_{0}=(x_{0},y_{0})$ y $P_{1}=(x_{1},y_{1})$ determinan una recta:
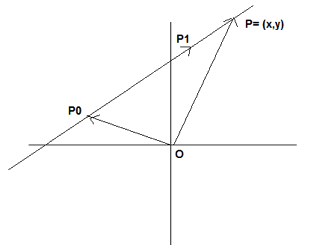
Sea $P$ un punto arbitrario de la recta que pasa por $P_{0}$ y $P_{1}$. Del diagrama anterior, se observa que: $\overrightarrow{0P_{0}}+\overrightarrow{P_{0}P}=\overrightarrow{0P}$ y además $\overrightarrow{P_{0}P}=\lambda \cdot \overrightarrow{P_{0}P_{1}}$ para algún $\lambda \in \mathbb{R}$
En consecuencia,
$\overrightarrow{0P_{0}}+\lambda \cdot \overrightarrow{P_{0}P_{1}}=\overrightarrow{0P}$ para $\lambda \in \mathbb{R}$ (*)
La ecuación (*) se llama ecuación vectorial de la recta. También puede expresarse de la forma
$(x_{0},y_{0})+\lambda \cdot (x_{1}-x_{0},y_{1}-y_{0})=(x,y)$ para $\lambda \in \mathbb{R}$
Tomado de: Barrantes, G (1974). Matemática undécimo año: Algebra vectorial.
Volver a lo básico
Durante el congreso del ICMI (International Comitte For Mathematical Instruction) en Kalsruhe, Alemania, en 1976, el matemático Michel Atiyah plantó en su conferencia el rotundo fracaso de la reforma que se quiso implantar y propuso “volver a lo básico”.
Ya desde 1970, se comenzó a percibir que los cambios propuestos no daban los resultados esperados y para 1980 hubo un reconocimiento general de que se había exagerado mucho en las tendencias hacia la “Matemática moderna”, en lo que respecta al énfasis puesto en las estructuras abstractas de la ciencia.
En compensación con los excesos de la década de los sesentas el movimiento “volver a lo básico” privilegió la obtención de habilidades y procedimientos, alejándose del enfoque teórico y abstracto de la reforma anterior. El currículo para finales de la década de los setenta puede considerarse una reconstrucción de lo que se hacía antes de la reforma de la Matemática modernas. Véase ejemplo 4:
Ejemplo 4. Material utilizado a finales de la década de los setentas.

Note en el ejemplo que se regresa al currículo que se trabajó hasta finales de los años cincuenta. Se agrega al final una sección relacionada con la resolución de problemas, que muchas veces por motivo de tiempo no se cubría en clase.
En esta línea, aparecieron diversos trabajos entre los que podemos mencionar a Morris Kline (1973) y Hans Freudenthal (1971).
Morris Kline estaba convencido de que era más fácil interesar a los y las jóvenes por los problemas reales que por la Matemática abstracta, sugirió sustituir el orden habitual de los contenidos por la presentación de conceptos y técnicas que se iban precisando para cada objetivo planteado, tratando de estructurar el currículo alrededor de la resolución de problemas. La propuesta hoy sigue vigente. Considerada más importante desarrollar la intuición que las demostraciones en los y las estudiantes; los argumentos heurísticos y los razonamientos por analogía deberían preceder a las bases formales. La demostración sería el paso final del proceso.
Por otro lado, los trabajos de Freudenthal dieron origen a la Educación Matemática Realista (EMR), enfoque en el cual se utilizaban situaciones del mundo real o problemas contextualizados como punto inicial para aprender matemática. La EMR se apoyaba en el uso de modelos que serían de mediación entre lo abstracto y lo concreto, y la interacción en el aula entre el alumnado y entre docentes y estudiantes.
Freudenthal planteó que la mejor forma de aprender y enseñar Matemática era en grupos pequeños y heterogéneos. Al trabajar de esta manera, los alumnos, guiados por los docentes, organizaban situaciones problemáticas y reflexionaban acerca de su actividad matematizadora. (Santamaría, 2006, pp.11-12)
Material didáctico producido por la Universidad Estatal a Distancia de Costa Rica. Créditos.