Resolución del problema
El trabajo $W$ viene dado por la integral $W = \int_a^b f\left( x \right)dx$ , en este caso se debe calcular la integral $W = \int_1^2 {\frac{10x}{\left ( \sqrt{x+1} \right )^5}} dx$ por los métodos solicitados.
Software
Cálculo de la integral utilizando el software WolframAlpha.
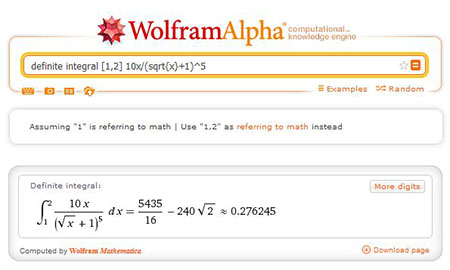
Cálculo de la integral utilizando Derive.
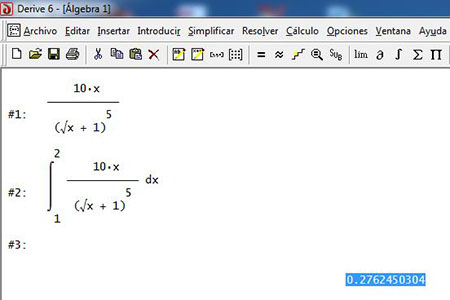
Cálculo de la integral utilizando Maxima.
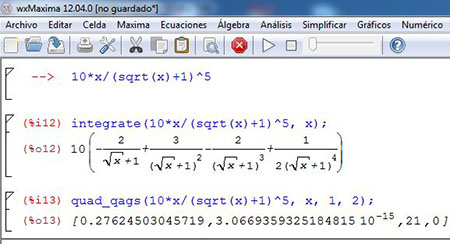
En este caso, la función quad_qags brinda cuatro datos en el resultado:
- La aproximación de la integral.
- El error absoluto de la aproximación.
- El número de veces que se evaluó el integrando.
- Un código de error, si existieron problemas en el cálculo.
Regla del Trapecio Compuesto para n=6
Calcular el tamaño de los subintervalos, $h = \frac{{2 - 1}}{6} = \frac{1}{6} = 0.1666666$.Construir una tabla en Excel para calcular la integral. En la figura adjunta se muestran los cálculos realizados:
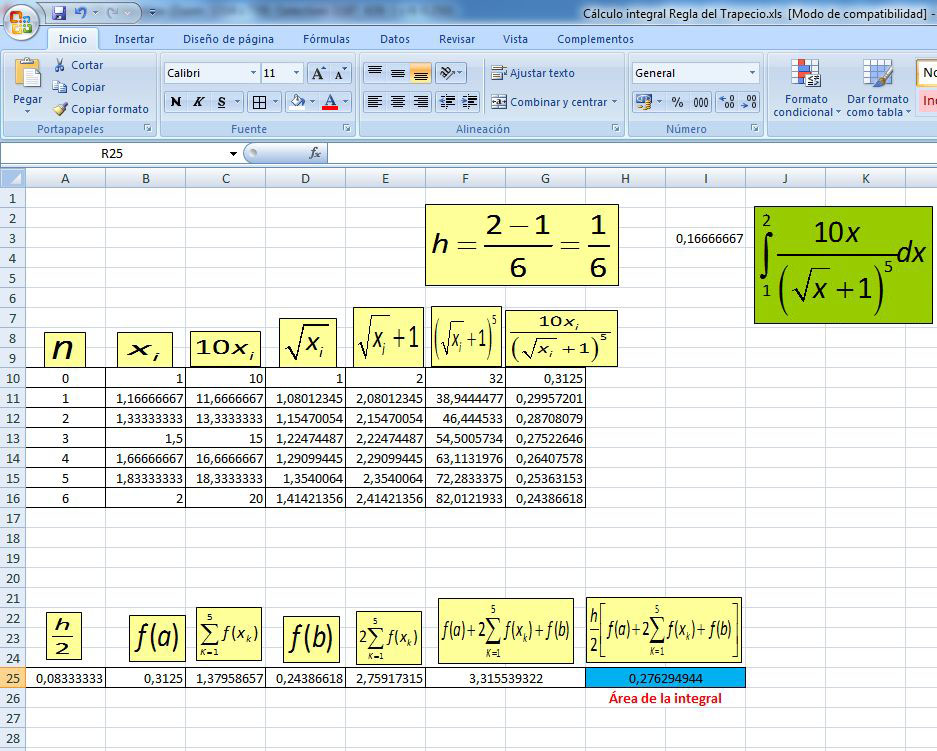
En Winplot se muestra el cálculo del área bajo la curva dada. Observe que las aproximaciones obtenidas son muy similares.
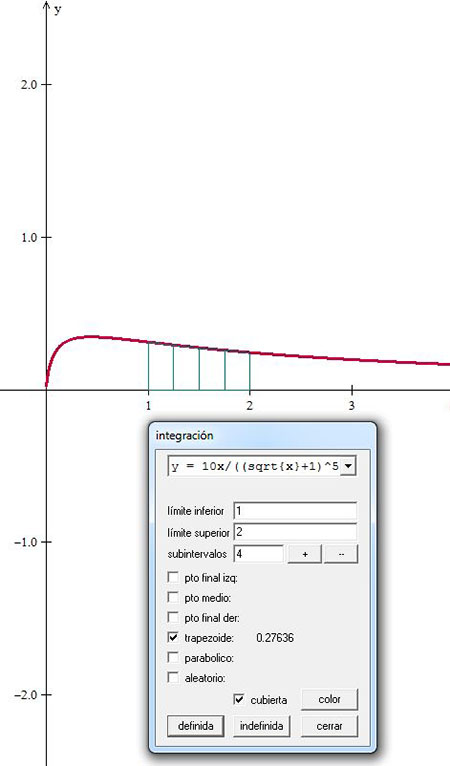
Regla de Simpson
Para la regla de Simpson 1/3, se tiene:
$a = 1$
${x_m} = \frac{{2 + 1}}{2} = \frac{3}{2}$
$b = 2$
$h = \frac{{2 - 1}}{2} = \frac{1}{2}$
$f\left( 1 \right) = \frac{{10 \bullet 1}}{{{{\left( {\sqrt 1 + 1} \right)}^5}}} = 0.3125$
$f\left( {1.5} \right) = \frac{{10 \bullet 1.5}}{{{{\left( {\sqrt {1.5} + 1} \right)}^5}}} = 0.2752264622$
$f\left( 2 \right) = \frac{{10 \bullet 2}}{{{{\left( {\sqrt 2 + 1} \right)}^5}}} = 0.2438661764$
Luego, al aplicar la regla de Simpson 1/3 se obtiene:
$W = \int_1^2 \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx \approx \frac{1}{3} \bullet \frac{1}{2}\left[ {f\left( 1 \right) + 4f\left( {1,5} \right) + f\left( 2 \right)} \right]$
$W = \int_1^2 \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx \approx \frac{1}{6}\left[ {0.3125 + 4 \bullet \left( {0.2752264622} \right) + 0.2438661764} \right]$
$W = \int_1^2 \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx \approx 0.2762120042$
En el software Winplot se muestra el área bajo la curva de $f\left( x \right) = \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}$ en el intervalo $\left[ {1,2} \right]$.
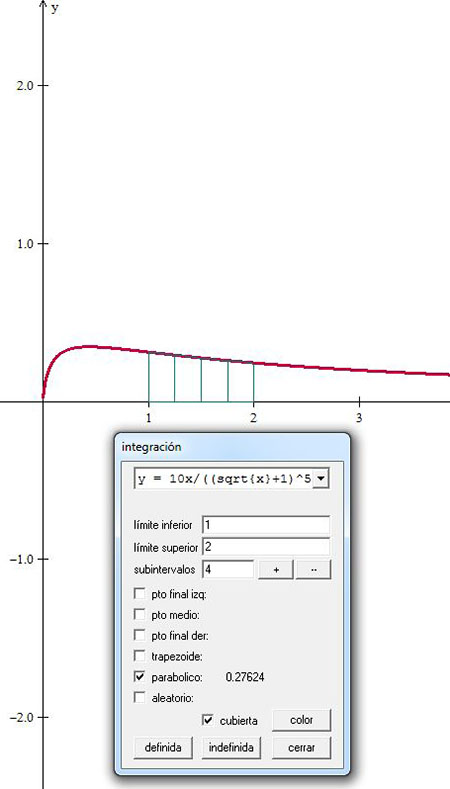
Regla de Simpson 3/8
En el caso de la regla de Simpson 3/8, se tiene:
$h = \frac{{2 - 1}}{3} = \frac{1}{3}$
$a = 1$
${x_m} = 1 + \frac{1}{3} = \frac{4}{3}$
${x_n} = \frac{4}{3} + \frac{1}{3} = \frac{5}{3}$
$b = 2$
$f\left( 1 \right) = \frac{{10 \bullet 1}}{{{{\left( {\sqrt 1 + 1} \right)}^5}}} = 0.3125$
$f\left( {\frac{4}{3}} \right) = \frac{{10 \bullet \frac{4}{3}}}{{{{\left( {\sqrt {\frac{4}{3}} + 1} \right)}^5}}} = 0.287080792$
$f\left( {\frac{5}{3}} \right) = \frac{{10 \bullet \frac{5}{3}}}{{{{\left( {\sqrt {\frac{5}{3}} + 1} \right)}^5}}} = 0.2640757764$
$f\left( 2 \right) = \frac{{10 \bullet 2}}{{{{\left( {\sqrt 2 + 1} \right)}^5}}} = 0.2438661764$
$W = \int_1^2 \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx \approx \frac{3}{8} \bullet \frac{1}{3}\left[ {f\left( 1 \right) + 3f\left( {\frac{4}{3}} \right) + 3f\left( {\frac{5}{3}} \right) + f\left( 2 \right)} \right]$
$W = \int_1^2 \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx \approx \frac{1}{8}\left[ {0.3125 + 3\left( {0.287080792} \right) + 3\left( {0.2640757764} \right) + 0.2438661764} \right]$
$W = \int_1^2{ \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}dx} \approx 0.2762294852$
En la tabla, se resumen los resultados obtenidos con diferentes métodos y asistentes matemáticos:
Método |
Valor |
WolframAlpha |
0.276245 |
Derive |
0.2762450304 |
Máxima |
0.27624503045719 |
Regla del trapecio (Excel) |
0.276294944 |
Winplot (Trapezoide) |
0.27636 |
0.2762120042 |
|
Winplot (Parabólico ) |
0.27624 |
0.2762294852 |
Del cuadro se concluye que $W \approx 0.2762$.