Descripción del método
En los cursos de Cálculo Integral aprendemos a calcular una integral definida de una función continua haciendo uso del Teorema Fundamental del Cálculo que dice que si $f\left( x \right)$ es una función continua en un intervalo [a, b] y $F\left( x \right)$ es una antiderivada de $f\left( x \right)$ entonces:
$\int_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)$
El problema en la práctica se presenta, cuando se nos hace imposible mediante métodos analíticos determinar la antiderivada requerida, aun cuando se trate de integrales aparentemente sencillas como $\int_1^2 {{{{x^3}} \over {1 + \sqrt x }}dx} $, que son imposibles de resolver con el Teorema Fundamental del Cálculo.
En estos casos, debemos de recurrir a la integración numérica que permite obtener aproximaciones bastantes exactas y que se pueden resolver con el uso de asistentes matemáticos como Maxima, Derive, Mathematica, entre otros.
En este módulo nos referiremos a la regla del trapecio y a la regla de Simpson.
Regla del trapecio
La regla del trapecio es uno de los métodos más utilizados para calcular aproximaciones numéricas de integrales definidas. Es la primera de las fórmulas cerradas de integración de Newton – Cotes, para el caso cuando el polinomio interpolante es de grado uno.
Para el polinomio interpolante de primer grado se tiene:
$A = \int_a^b {f\left( x \right)dx} \cong \int_a^b {{f_1}\left( x \right)dx} $, donde
${f_1}\left( x \right) = f\left( a \right) + {{f\left( b \right) - f\left( a \right)} \over {b - a}}\left( {x - a} \right)$
Precisamente el área bajo la recta es una aproximación de la integral $\int_a^b {f\left( x \right)dx} $, es decir que $A = \int_a^b {\left[ {f\left( a \right) + {{f\left( b \right) - f\left( a \right)} \over {b - a}}\left( {x - a} \right)} \right]dx} $. Luego se tiene que la regla del trapecio viene dada por la fórmula:
$A = \int_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{{f\left( a \right) + f\left( b \right)} \over 2}} \right] $
El nombre regla del trapecio se debe a la interpretación geométrica que se hace de la fórmula. Cuando el polinomio interpolante es de grado uno, su gráfica representa una línea recta en el intervalo [a, b] que es el área del trapecio que se forma, como se muestra en la figura.
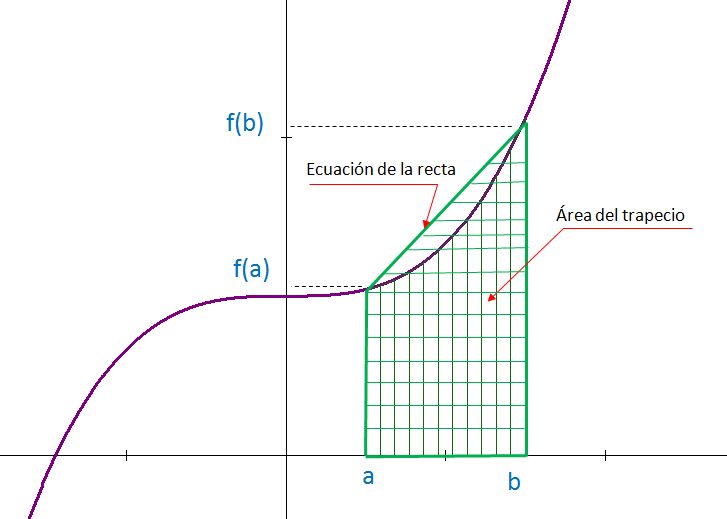
Ejemplo 1
Calcular la integral de $f\left( x \right) = {x^3} - 6{x^2} + 11x - 6$, en el intervalo [1.3, 1.8] aplicando la regla del trapecio.
Solución
- Con la ayuda de una calculadora, evaluar la función en los extremos del intervalo $f\left( {1.3} \right) = 0.357$, $f\left( {1.8} \right) = 0.192$
- Calcular $b - a = 1.8 - 1.3 = 0.5$
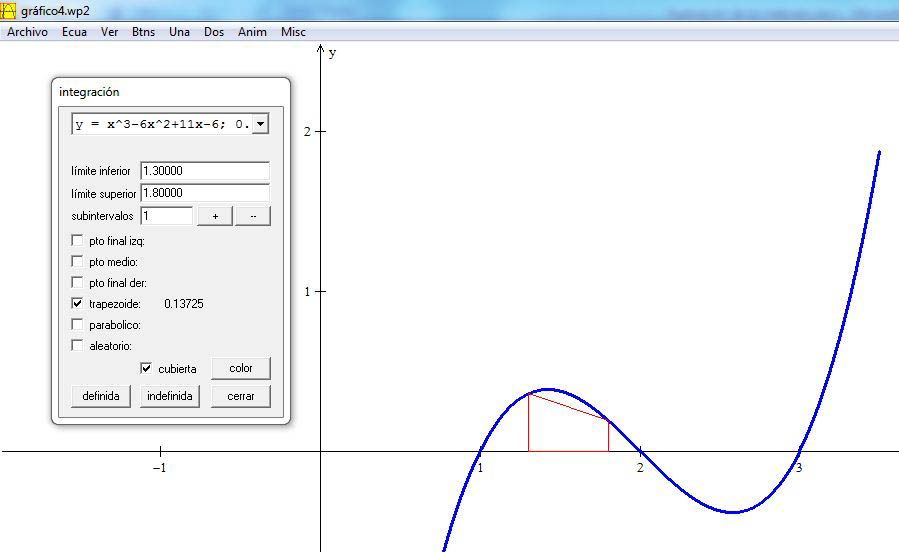
- Aplicar la fórmula de la regla del trapecio $A = \int_{1.3}^{1.8} {\left( {{x^3} - 6{x^2} + 11x - 6} \right)dx} \cong 0.5\left[ {{{0.357 + 0.192} \over 2}} \right] = 0.13725$
En la siguiente figura se muestra la gráfica de la función construida con el software libre Winplot.
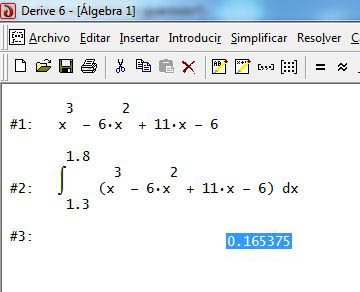
Cabe mencionar que el valor real de esta integral es aproximadamente 0.165375, como se muestra en la hoja de trabajo de Derive.
Error de la regla del trapecio
Del ejemplo anterior se puede observar que si la función a integrar no es lineal, la regla del trapecio genera un error. La fórmula para calcular el error de truncamiento local de una sola aplicación de la regla del trapecio viene dada por:
${E_x} = - {1 \over {12}}{f^{\left( 2 \right)}}\left( \xi \right){\left( {b - a} \right)^3}$
El valor $\xi $ se encuentra en algún lugar del intervalo [a, b]. Si la función a integrar es lineal, entonces la regla del trapecio será exacta.
En el ejemplo se tiene que $ \xi = 0.5 $ y ${f^{\left( 2 \right)}}\left( x \right) = 6x - 12 $, luego ${f^{\left( 2 \right)}}\left( {0.5} \right) = - 9 $. El error viene dado por: $ {E_x} = - {1 \over {12}} \cdot \left( { - 9} \right) \cdot {\left( {0.5} \right)^3} = 0.09375 $, lo que indica que, en las funciones a integrar que posean derivadas de segundo orden o de orden superior, la regla del trapecio genera un error.
Regla del trapecio compuesta
Para obtener una mejor aproximación de la integral con este método, la regla del trapecio se puede ampliar si se subdivide el intervalo [a, b] en $n $ subintervalos, todos de la misma longitud $h = {{b - a} \over n}$. A este método se le conoce con el nombre de la regla del trapecio compuesta. Para aplicar este método siga los siguientes pasos:
- Divida el intervalo [a, b] en subintervalos de igual medida.
- Aproxime en cada subintervalo la función $f(x)$ por una recta.
- Aproxime el área bajo la curva $f $ en el intervalo [a, b] mediante la suma de las áreas de los trapecios.
- Aplique la regla del trapecio compuesta que viene dada por:
$\int_a^b {f\left( x \right)dx} \approx {h \over 2}\left[ {f\left( a \right) + 2\mathop \sum \limits_{k = 1}^{n - 1} f\left( {{x_k}} \right) + f\left( b \right)} \right]$
El error estimado viene dado por la fórmula:
${E_x} = - {{b - a} \over {12}}{h^2}{f^{\left( 2 \right)}}\left( \xi \right)$
Ejemplo 2
Calcular la integral de $f\left( x \right) = {x^3} - 6{x^2} + 11x - 6$, en el intervalo [1.3, 1.8] aplicando la regla del trapecio compuesta. Haga 6 subintervalos de igual longitud.
Solución
Calcular el tamaño de los subintervalos, $h = {{1.8 - 1.3} \over 6} = 0.083333$
Construir una tabla en Excel para calcular la integral. En la siguiente figura se muestran los cálculos realizados en esta hoja electrónica.
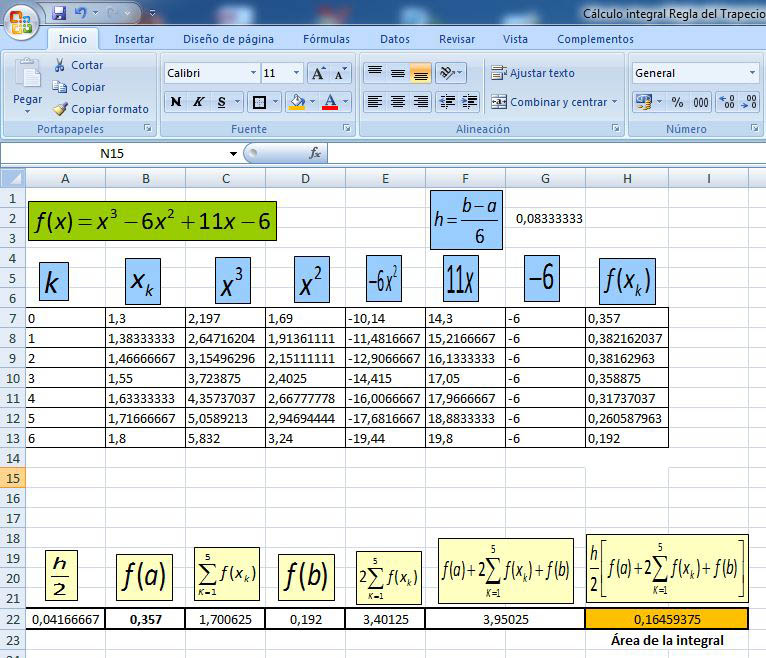
El error asociado en la aproximación es igual a: ${E_x} = - {{1.8 - 1.3} \over {12}} \cdot {\left( {0.08333333} \right)^2} \cdot \left( { - 11.50000} \right) = 3.327543x{10^{ - 3}}$.
El valor real de la integral es aproximadamente 0.165375 que es una mejor aproximación que la obtenida para $n = 1 $. Obsérvese la diferencia entre los errores obtenidos con la regla del trapecio simple y la compuesta.
Con la regla del trapecio también es posible calcular integrales cuya antiderivada no es posible obtener por los métodos analíticos tradicionales, como el que se muestra en el siguiente ejemplo.
Ejemplo 3
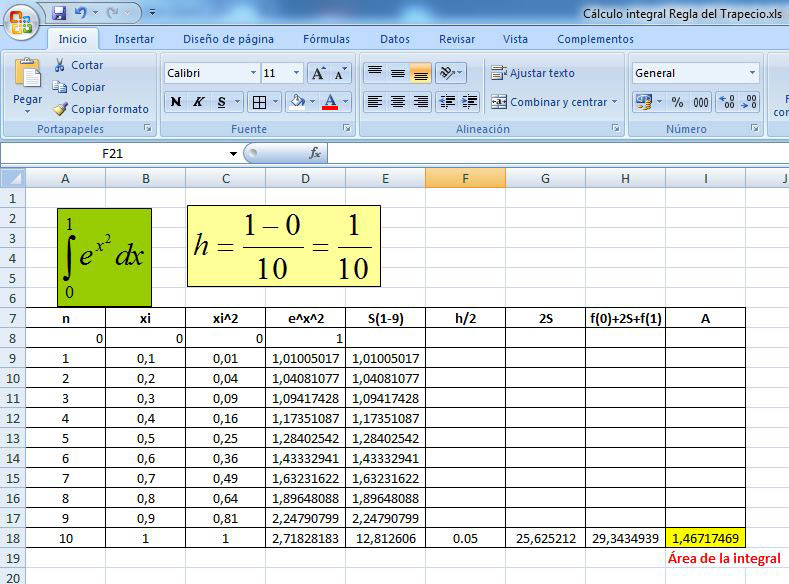
Calcular la integral de $f\left( x \right) = {e^{{x^2}}}$ en el intervalo [0, 1] aplicando la regla del trapecio compuesta. Haga 10 subintervalos de igual longitud.
Los cálculos se hicieron en Excel y los comandos utilizados son semejantes a los del ejemplo anterior, como se muestra en la figura adjunta.
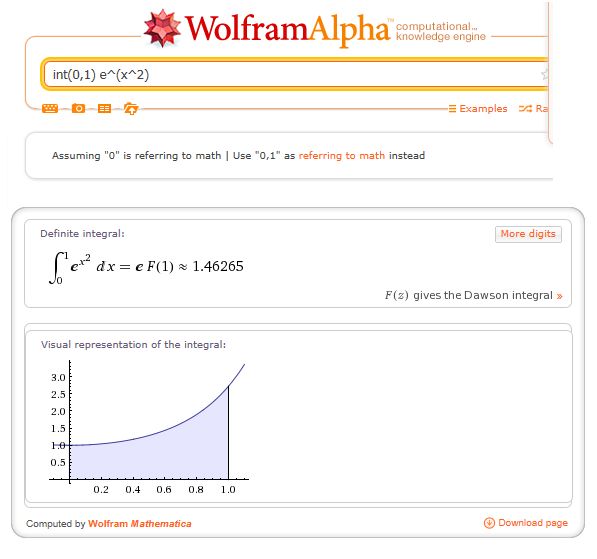
El valor real aproximado de la integral fue calculado en el software Wolfram Alpha como se muestra en la figura adjunta.
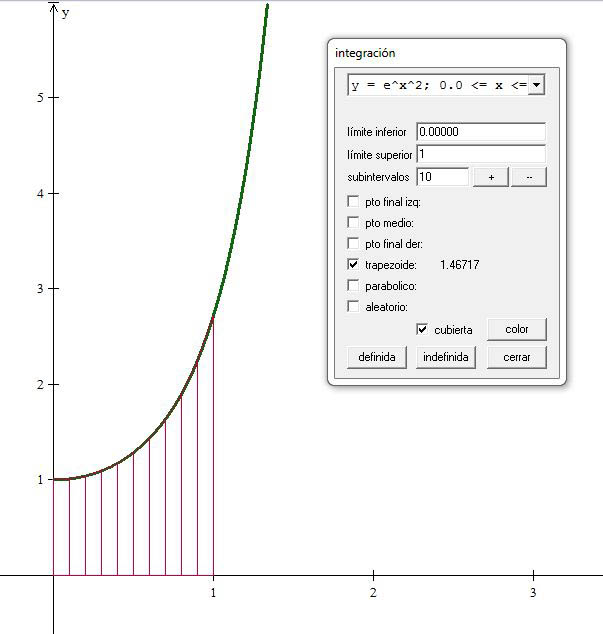
La gráfica de la función se muestra en la figura adjunta, construida en Winplot. Obsérvese el valor real aproximado del área bajo la curva.
El error asociado en la aproximación es igual a: ${E_x} = - {{1 - 0} \over {12}} \cdot {\left( {{1 \over {10}}} \right)^2}\left[ {2 \cdot {e^{{{\left( {{1 \over {10}}} \right)}^2}}} \cdot \left( {2 \cdot {{\left( {{1 \over {10}}} \right)}^2} + 1} \right)} \right] = - 1.717085284x{10^{ - 3}}$. Este error indica que la aproximación obtenida es aceptable.
Regla de Simpson
Además de la regla del trapecio, otra manera de obtener una estimación más exacta de una integral es utilizar polinomios de orden superior para conectar los puntos. Por ejemplo, se pueden conectar con un polinomio de tercer orden los puntos $f(a) $, $f(b) $ y el punto medio entre ellos. A las fórmulas que resultan de calcular la integral bajo estos polinomios se les llama reglas de Simpson.
Con la regla de Simpson es posible obtener una aproximación más precisa del área bajo una curva ya que se conectan grupos sucesivos de tres puntos sobre la curva mediante parábolas de segundo grado, y al sumar las áreas bajo las parábolas se obtiene el área aproximada bajo la curva.
Esta regla a diferencia de la regla del trapecio, donde a mayor número de subdivisiones se obtiene una mejor aproximación, lo que hace es ajustar una curva de orden superior en lugar de la línea recta como sucede con la regla del trapecio.
Suponga que se tiene la función $f(x) $ y los siguientes datos:
| $a$ | ${x_m}$ | $b$ |
| $f(a)$ | $f({x_m})$ | $f(b)$ |
Donde ${x_m}$ es el punto medio entre $a$ y $b$. Entonces es posible ajustar por puntos $f(a)$, $f(b)$ y $f({x_m})$ una parábola. De la misma forma, si existen dos puntos entre $f(a)$ y $f(b)$, entonces por esos cuatro puntos será posible ajustar una curva de grado tres, y así sucesivamente.
En la gráfica se muestra una parábola que aproxima a una función real. Observe que se calcula el área o la integral bajo la parábola que pasa por los tres puntos.

Así entonces para calcular el área bajo la curva aplicando la regla de Simpson se utiliza la siguiente fórmula:
$\int_a^b {f\left( x \right)dx} \approx {h \over 3}\left[ {f\left( a \right) + 4f\left( {{x_m}} \right) + f\left( b \right)} \right]$, con $h = {{b - a} \over 2}$
El error estimado viene dado por la fórmula:
${E_x} = - {{{h^5}} \over {90}}{f^{\left( 4 \right)}}\left( \xi \right)$
Observe que ${E_x}$ involucra la cuarta derivada, por lo que la regla es exacta para polinomios de grado menor o igual a tres.
Ejemplo 4
Calcular la integral de $f\left( x \right) = {e^{{x^2}}}$ en el intervalo [0, 1] aplicando la regla Simpson 1/3.
En este caso se tienen los siguientes datos:
$\eqalign{
& a = 0 \cr
& {x_m} = {{1 + 0} \over 2} = {1 \over 2} \cr
& b = 1 \cr
& h = {{1 - 0} \over 2} = {1 \over 2} \cr
& f\left( 0 \right) = {e^{{0^2}}} = 1 \cr
& f\left( {{1 \over 2}} \right) = {e^{{{\left( {{1 \over 2}} \right)}^2}}} = {e^{{1 \over 4}}} \cr
& f\left( 1 \right) = e \cr} $
Luego aplicando la regla de Simpson 1/3 se tiene que:
$\eqalign{
& \int_0^1 {{e^{{x^2}}}dx} \approx {1 \over 3} \cdot {1 \over 2}\left[ {f\left( 0 \right) + 4f\left( {{1 \over 2}} \right) + f\left( 1 \right)} \right] \cr
& \int_0^1 {{e^{{x^2}}}dx} \approx {1 \over 6}\left[ {1 + 4 \cdot {e^{{1 \over 4}}} + e} \right] \cr
& \int_0^1 {{e^{{x^2}}}dx} \approx 1.475730583 \cr} $
Observe que el valor obtenido con la regla de Simpson 1/3 es una mejor aproximación que el obtenido con la regla del trapecio. Para calcular el error, hay que determinar primero la cuarta derivada de la función, la cual viene dada por:
$\eqalign{
& f\left( x \right) = {e^{{x^2}}} \cr
& {f^{\left( 1 \right)}}\left( x \right) = 2x{e^{{x^2}}} \cr
& {f^{\left( 2 \right)}}\left( x \right) = 2{e^{{x^2}}}\left( {2{x^2} + 1} \right) \cr
& {f^{\left( 3 \right)}}\left( x \right) = 4x{e^{{x^2}}}\left( {2{x^2} + 3} \right) \cr
& {f^{\left( 4 \right)}}\left( x \right) = 4{e^{{x^2}}}\left( {4{x^4} + 12{x^2} + 3} \right) \cr } $
Luego ${E_x} = - {1 \over {90}} \cdot {\left( {{1 \over 2}} \right)^5}\left[ {4{e^{{{\left( {{1 \over 2}} \right)}^2}}}\left( {4{{\left( {{1 \over 2}} \right)}^4} + 12{{\left( {{1 \over 2}} \right)}^2} + 3} \right)} \right] = - 0.011146$
Regla de Simpson 3/8
De la misma manera como se hizo en la regla de trapecio, la regla de Simpson se puede ampliar si se subdivide el intervalo [a, b] en $n$ subintervalos, todos de la misma longitud $h = {{b - a} \over n}$. Cuando el número de subdivisiones que se haga sea igual a tres, entonces el método recibe el nombre de la Regla de Simpson 3/8. Se le da ese nombre debido al factor ${3 \over 8}h$ que aparece en la fórmula.
Suponga que se tiene la función $f(x)$ y los siguientes datos:
| $a$ | ${x_m}$ | ${x_n}$ | $b$ |
| $f(a)$ | $f({x_m})$ | $f({x_n})$ | $f(b)$ |
Donde ${x_m}$, ${x_n}$ son los puntos que dividen en tres partes iguales al intervalo [a, b].
En la gráfica se muestra una parábola que aproxima a una función real. Observe que se calcula el área o la integral bajo la parábola que pasa por los cuatro puntos.

Para calcular el área bajo la curva aplicando la regla de Simpson 3/8 se utiliza la siguiente fórmula:
$\int_a^b {f\left( x \right)dx} \approx {3 \over 8}h\left[ {f\left( a \right) + 3f\left( {{x_m}} \right) + 3f\left( {{x_n}} \right) + f\left( b \right)} \right]$, con $h = {{b - a} \over 3}$
Es importante señalar que para la regla de Simpson 3/8 compuesta, el número de subintervalos solo puede ser un múltiplo de 3, en caso contrario no es posible aplicar la regla.
El error estimado viene dado por la fórmula:
${E_x} = - {{3{h^5}} \over {80}}{f^{\left( 4 \right)}}\left( \xi \right)$
Ejemplo 5
Calcular la integral de $f\left( x \right) = {e^x}\ln x$ en el intervalo [1, 3] aplicando la regla Simpson 3/8.
En este caso se tienen los siguientes datos:
$\eqalign{
& h = {{3 - 1} \over 3} = {2 \over 3} \cr
& a = 1 \cr
& {x_m} = 1 + {2 \over 3} = {5 \over 3} \cr
& {x_n} = {5 \over 3} + {2 \over 3} = {7 \over 3} \cr
& b = 3 \cr
& f\left( 1 \right) = {e^1}\ln 1 = 0 \cr
& f\left( {{5 \over 3}} \right) = {e^{{5 \over 3}}} \cdot ln\left( {{5 \over 3}} \right) = 2.7045611 \cr
& f\left( {{7 \over 3}} \right) = {e^{{7 \over 3}}} \cdot ln\left( {{7 \over 3}} \right) = 8.7375545 \cr
& f\left( 3 \right) = {e^3} \cdot ln\left( 3 \right) = 22.06621769 \cr } $
Luego aplicando la regla de Simpson 3/8 se tiene que:
$\eqalign{
& \int_1^3 {{e^x}\ln x} dx \approx {3 \over 8} \cdot {2 \over 3}\left[ {f\left( 1 \right) + 3f\left( {{5 \over 3}} \right) + 3f\left( {{7 \over 3}} \right) + f\left( 3 \right)} \right] \cr
& \int_1^3 {{e^x}\ln x} dx \approx {1 \over 4}\left[ {0 + 3\left( {2.7045611} \right) + 3\left( {8.7375545} \right) + 22.06621769} \right] \cr
& \int_1^3 {{e^x}\ln x} dx \approx 14.09814112 \cr} $
En el graficador Winplot se muestra la gráfica de la curva $f\left( x \right) = {e^x}\ln x$. Observe el valor obtenido.
Luego ${E_x} = - {3 \over {80}} \cdot {\left( {{1 \over 2}} \right)^5}\left[ {4{e^{{{\left( {{1 \over 2}} \right)}^2}}}\left( {4{{\left( {{1 \over 2}} \right)}^4} + 12{{\left( {{1 \over 2}} \right)}^2} + 3} \right)} \right] = - 0.0376179$
Resumen
A continuación, se resumen los métodos estudiados.
Regla del trapecio
Fórmula: $A = \int_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{{f\left( a \right) + f\left( b \right)} \over 2}} \right] $
Error: ${E_x} = - {1 \over {12}}{f^{\left( 2 \right)}}\left( \xi \right){\left( {b - a} \right)^3}$
Regla del trapecio compuesta
Fórmula: $\int_a^b {f\left( x \right)dx} \approx {h \over 2}\left[ {f\left( a \right) + 2\mathop \sum \limits_{k = 1}^{n - 1} f\left( {{x_k}} \right) + f\left( b \right)} \right]$
Error: ${E_x} = - {{b - a} \over {12}}{h^2}{f^{\left( 2 \right)}}\left( \xi \right)$
Regla de Simpson 1/3
Fórmula: $\int_a^b {f\left( x \right)dx} \approx {h \over 3}\left[ {f\left( a \right) + 4f\left( {{x_m}} \right) + f\left( b \right)} \right]$, con $h = {{b - a} \over 2}$
Error: ${E_x} = - {{{h^5}} \over {90}}{f^{\left( 4 \right)}}\left( \xi \right)$
Regla de Simpson 3/8
Fórmula: $\int_a^b {f\left( x \right)dx} \approx {3 \over 8}h\left[ {f\left( a \right) + 3f\left( {{x_m}} \right) + 3f\left( {{x_n}} \right) + f\left( b \right)} \right]$, con $h = {{b - a} \over 3}$
Error: ${E_x} = - {{3{h^5}} \over {80}}{f^{\left( 4 \right)}}\left( \xi \right)$