Introducción

Integración numérica
Es una técnica matemática que se utiliza principalmente en las ciencias y en las ingenierías, para obtener valores aproximados de integrales definidas que no pueden calcularse mediante métodos analíticos tradicionales.
Por ejemplo, si se quiere determinar el trabajo realizado por un cuerpo que se desplaza linealmente, a partir del reposo, con una fuerza variable dada por $f(x) = \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}$ , desde los 5 hasta los 10 metros, se tendría que calcular la integral $\int_5^{10} {f(x)dx} $, lo cual, como se expuso anteriormente, no es posible hacerlo ni mediante métodos tradicionales de integración ni por medio del teorema fundamental del cálculo.
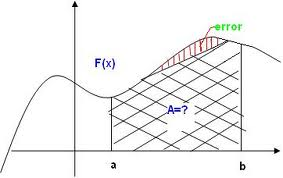
Existen varios métodos de integración numérica, en este módulo se estudiarán la regla del trapecio y la de Simpson.
Para desarrollar lo propuesto en este módulo, se estudiará lo siguiente:
-
La resolución del problema con comandos y funciones del software.
-
Una propuesta metodológica, para que el futuro docente visualice cómo puede desarrollar el tema en la educación secundaria.