Propuesta metodológica
Cálculo del área de una superficie de revolución generada por la curva $y = f\left( x \right)$
Justificación
En un mundo globalizado es necesario que los sistemas educativos permitan el desarrollo de competencias educativas y profesionales, que potencien el uso de las Tecnologías de la Información y la Comunicación en todas las actividades del quehacer cotidiano. Por eso, es importante que el futuro profesor de matemática no solo tenga conocimiento de softwares especializados, sino que también los utilice en la mediación pedagógica para el tratamiento de los contenidos. Software como: Maple, Derive, Maxima, Winplot, Mathematica, Matlab, Wolfram alfa, entre otros; son muy útiles en matemática, por lo tanto, es primordial que el docente los integre en su trabajo académico.
El cálculo diferencial e integral, son dos de las disciplinas de la matemática que más aplicaciones tienen en el mundo cotidiano; por ejemplo, con el cálculo integral se pueden determinar diferentes valores, como: áreas entre curvas, volúmenes de sólidos, el trabajo realizado por una fuerza variable, entre otros. Específicamente, en el campo de la ingeniería, se puede calcular la tensión de los cables de los puentes colgantes, de las líneas de transmisión, de los cables que sujetan a los teleféricos, de los contravientos para torres altas, por citar algunos ejemplos.
Conocimientos previos
- Conocimientos básicos de cálculo diferencial.
- Conocimientos básicos de cálculo integral.
Objetivos
- Calcular el área de la superficie que se obtiene al girar la curva $y = x^2$ en el intervalo $\left[ {0,2} \right]$ alrededor del eje $x$, utilizando la integración algebraica.
- Calcular el área de la superficie que se obtiene al girar la curva $y = x^2$ en el intervalo $\left[ {0,2} \right]$ alrededor del eje $x$, utilizando la regla del trapecio compuesta para $n=6$.
- Calcular el área de la superficie que se obtiene al girar la curva $y = x^2$ en el intervalo $\left[ {0,2} \right]$alrededor del eje $x$, utilizando la regla de Simpson 3/8.
Contenidos
- Integración algebraica.
- Regla del trapecio compuesta para $n=6$.
- Regla de Simpson 3/8.
Actividades
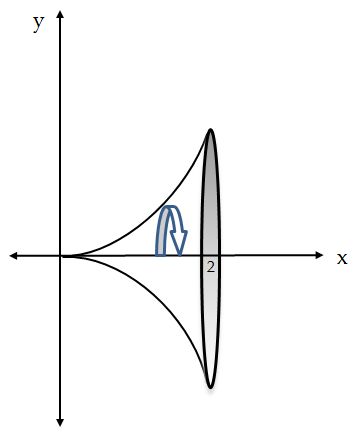
1. Solicite a los estudiantes que hagan una representación gráfica del sólido generado por la curva $y = x^2$ alrededor del eje $x$ en el intervalo $\left[ {0,2} \right]$.
2. Comente que si se tiene una curva $y = f\left( x \right)$ continua en un intervalo $\left[ {a,b} \right]$ y derivable en $\left] {a,b} \right[$, entonces, al girar esa curva alrededor del eje x el área que se obtiene viene dada por la integral $A = 2\pi \int_a^b {{f(x)\sqrt{1+\left \{ f'(x) \right \}^2}} dx}$ .
3. Solicite a los estudiantes que, de acuerdo con lo anterior, calculen algebraicamente el área de la superficie que genera la curva $y = x^2$ en el intervalo [0,2]. Para esto, deben resolver la integral $A = 2\pi \int_a^b {{f(x)\sqrt{1+\left \{ f'(x) \right \}^2}} dx}$. En esta parte de la actividad, los alumnos llegarán a la conclusión de que este es uno de los tantos ejemplos de integrales donde no es posible hacer el cálculo de la primitiva con los métodos de integración tradicional. En la figura adjunta, se muestra la antiderivada para la integral $A = 2\pi \int_a^b {{f(x)\sqrt{1+\left \{ f'(x) \right \}^2}} dx}$, con el software Maxima.
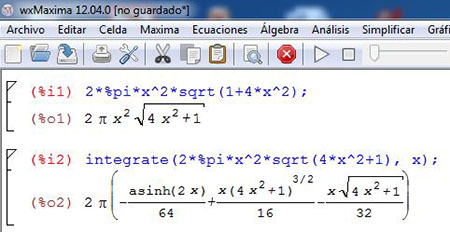
Es importante que el docente resalte la importancia del uso de software especializado en el cálculo de este tipo de expresiones matemáticas.
4. Exponga que existen muchas integrales cuya antiderivada es difícil de calcular con los métodos tradicionales de integración, por lo cual hay que recurrir a software especializado o a métodos de integración numérica, como los estudiados en este módulo. Por ejemplo, los estudiantes pueden utilizar Winplot para construir la gráfica de la función en el intervalo dado y calcular el valor de la integral, como se muestra en la figura adjunta.
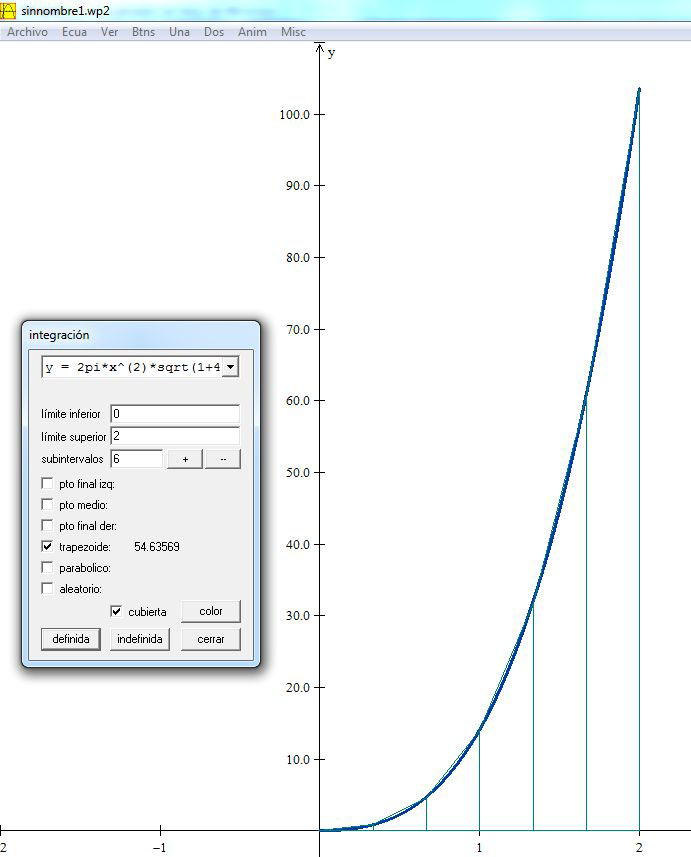
Señale a los estudiantes que, en este caso, se hace uso de la regla del trapecio compuesta con seis subintervalos (n6).
5. Solicite a los estudiantes que calculen el valor de la integral con la regla del trapecio compuesta. Además, pídales que utilicen diferentes cantidades de subintervalos, para ello recuérdeles la fórmula:
$$\int_{b}^{a}{{f(x)}dx} \approx \frac{h}{2}\left [ f(a) + 2 \sum_{k=1}^{n-1}f(x_k) + f(b) \right ]$$
Después, pueden comparar los resultados obtenidos y sacar conclusiones sobre si el número de subintervalos influye en la aproximación que se obtenga. En una hoja de trabajo Excel pueden hacer los cálculos respectivos para seis subintervalos, como se muestra en la figura adjunta.
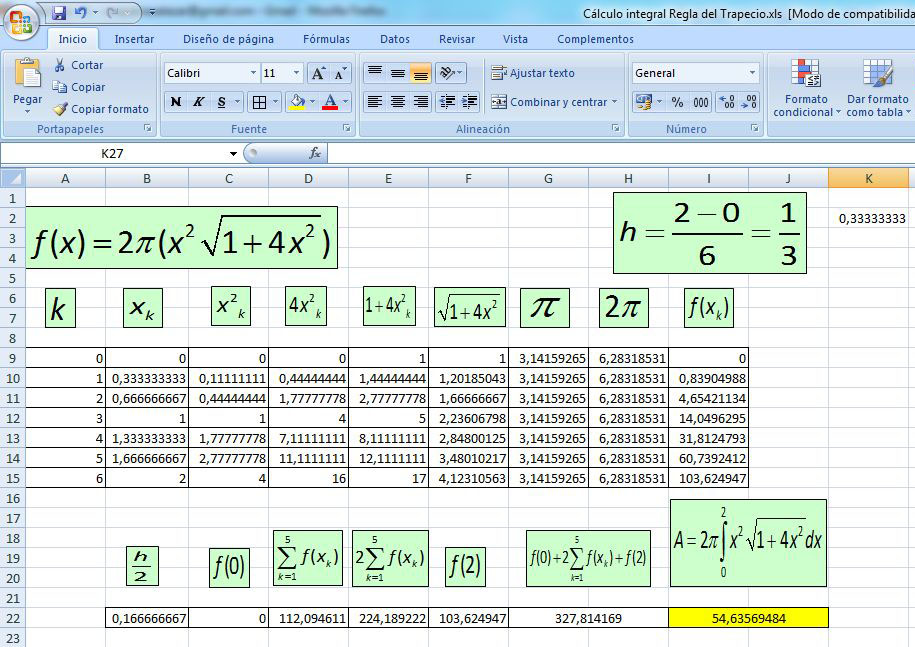
6. Luego, solicite a los estudiantes que calculen la integral con alguno de los programas señalados anteriormente. La integral de la propuesta está calculada en Derive y en Maxima, como se muestra en la figura adjunta.
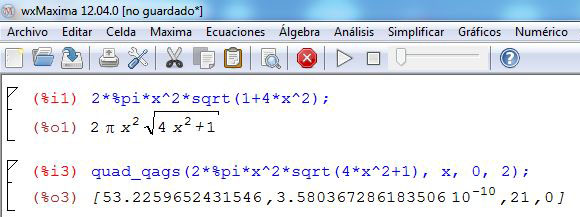
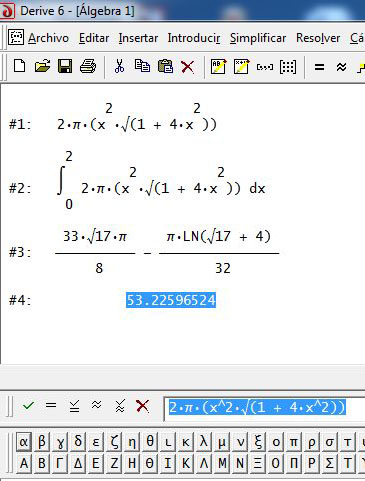
7. En esta parte de la actividad puede plantear a los estudiantes preguntas como: ¿por qué los resultados obtenidos en Winplot y en Excel casi no varían?, ¿por qué hay diferencia en las aproximaciones obtenidas en Excel, Derive y Maxima?, ¿qué sucede cuando el número de subintervalos tiende a infinito?, ¿ se obtendría una mejor aproximación de la integral?, ¿por qué en la regla de Simpson 3/8 compuesta el número de subintervalos  solo puede ser un múltiplo de 3? (en este caso, deben justificar la respuesta).
solo puede ser un múltiplo de 3? (en este caso, deben justificar la respuesta).
8. Luego, solicite a los estudiantes que hagan el cálculo de la integral, pero utilizando la regla de Simpson 3/8. Después, pida que comparen los resultados obtenidos con los dos métodos y que le comuniquen las conclusiones obtenidas de la actividad realizada.
9. También, se pueden discutir las ventajas y desventajas de cada uno de los métodos; asimismo, en qué circunstancias se recomienda usar uno u otro.Repita la actividad con otras integrales. Genere la discusión en el grupo, para obtener una conclusión general de la actividad.
Diseñe propuestas de mediación, donde los estudiantes hagan uso de la integración numérica para resolver problemas, en los cuales apliquen las siguientes integrales:
Volumen |
$V = \int_{a}^{b} {{A(x)}dx}$ |
Volumen de un sólido de revolución |
$V = 2\pi \int_{a}^{b} {{x f(x)}dx}$ |
Trabajo |
$T= \int_{a}^{b} {{F(x)}dx}$ |
Área de una superficie de revolución que gira alrededor del eje $x$ |
$A = 2\pi \int_a^b {{f(x)\sqrt{1+\left \{ f'(x) \right \}^2}} dx}$ |
Longitud de una curva |
$L = \int_a^b {{\sqrt{1+\left \{ f'(x) \right \}^2}} dx}$ |
Volumen de un sólido de revolución generado entre dos curvas que gira alrededor del eje x |
$V = \pi \int_{a}^{b} \left( \left[ f(x) \right] ^2 - \left [ g(x) \right ]^2 \right) dx$ |
Pida a los estudiantes que traigan a la clase problemas de su entorno local, en los cuales se haga uso de la integración numérica, que tengan que ver con el medio ambiente, la economía y la salud. Pueden investigar en Internet, en las fábricas de su comunidad, con los líderes comunales, con los profesionales de la Escuela de Ciencias Exactas y Naturales, en la Escuela de Administración de la UNED, entre otros.