Módulo 4: Aproximación de integrales
Polinomio interpolante
Para un conjunto de números diferentes ${x_0},{x_1},...,{x_n},\left( {n + 1,n \geqslant 0} \right)$ y una función $f$ cuyos valores están dados en estos puntos, existe un único polinomio ${P_n}\left( x \right)$ de grado menor o igual que $n$ , tal que $f\left( {{x_k}} \right) = P\left( {{x_k}} \right)$, para $k = 0,1,...,n$. El polinomio $P\left( x \right)$ se llama polinomio interpolante.
Regla del trapecio
Método de integración para calcular integrales definidas donde el polinomio interpolante es de grado uno. Se utiliza la fórmula $A = \int_a^b f\left( x \right)dx \approx \left( {b - a} \right)\left[ {\frac{{f\left( a \right) + f\left( b \right)}}{2}} \right]$.
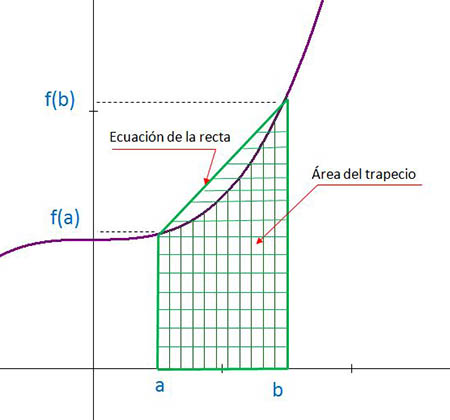
Regla del trapecio compuesta
Es una generalización de la regla de trapecio para obtener una mejor aproximación de la integral y consiste en subdividir el intervalo $\left[ {a,b} \right]$ en $n$ subintervalos, todos de la misma longitud $h = \frac{{b - a}}{n}$. Se aplica la fórmula $ \int_a^b f\left( x \right)dx \approx \frac{h}{2}\left[ {f\left( a \right) + 2\mathop \sum \limits_{k = 1}^{n - 1} f\left( {{x_k}} \right) + f\left( b \right)} \right]$.
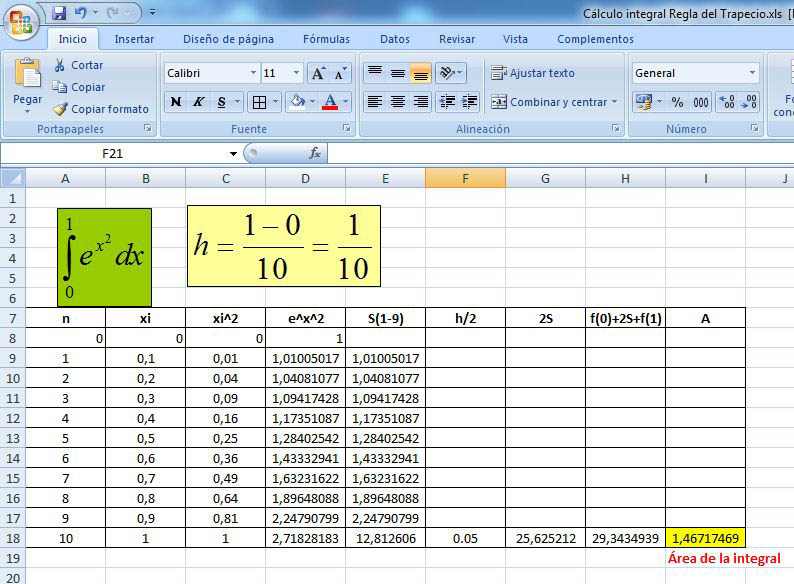
Error regla del trapecio
Cuando la función a integrar sea de grado mayor o igual a dos, la regla del trapecio genera un error de truncamiento local. La fórmula del error de truncamiento local en una sola aplicación viene dada por ${E_x} = - \frac{1}{{12}}{f^{\left( 2 \right)}}\left( \xi \right){\left( {b - a} \right)^3}$.
Regla de Simpson 1/3
Método de integración para calcular integrales definidas donde se conectan grupos sucesivos de tres puntos sobre la curva mediante parábolas de segundo grado. A las fórmulas que resultan de calcular la integral bajo estos polinomios se les llama Reglas de Simpson. Se utiliza la fórmula $\int_a^b f\left( x \right)dx \approx \frac{h}{3}\left[ {f\left( a \right) + 4f\left( {{x_m}} \right) + f\left( b \right)} \right]$ con $h = \frac{{b - a}}{2}$.
Error Regla de Simpson 1/3
Error de truncamiento que se genera al aplicar la regla. La fórmula del error de truncamiento local en una sola aplicación viene dada ${E_x} = - \frac{{{h^5}}}{{90}}{f^{\left( 4 \right)}}\left( \xi \right)$.
Regla de Simpson 3/8
Es una generalización de la regla de trapecio para obtener una mejor aproximación de la integral y consiste en subdividir el intervalo $\left[ {a,b} \right]$ en $n$ subintervalos, todos de la misma longitud $h = \frac{{b - a}}{n}$. Cuando el número de subdivisiones que se haga sea igual a tres, entonces el método recibe el nombre de la regla de Simpson 3/8.
Se utiliza la fórmula $\int_a^b {f\left( x \right)dx \approx \frac{3}{8}h\left[ {f\left( a \right) + 3f\left( {{x_m}} \right) + 3f\left( {{x_n}} \right) + f\left( b \right)} \right]} $ con $h = \frac{{b - a}}{3}$. En la Regla de Simpson 3/8 compuesta, el número de subintervalos 
solo puede ser un múltiplo de 3, en caso contrario no es posible aplicar la regla.
