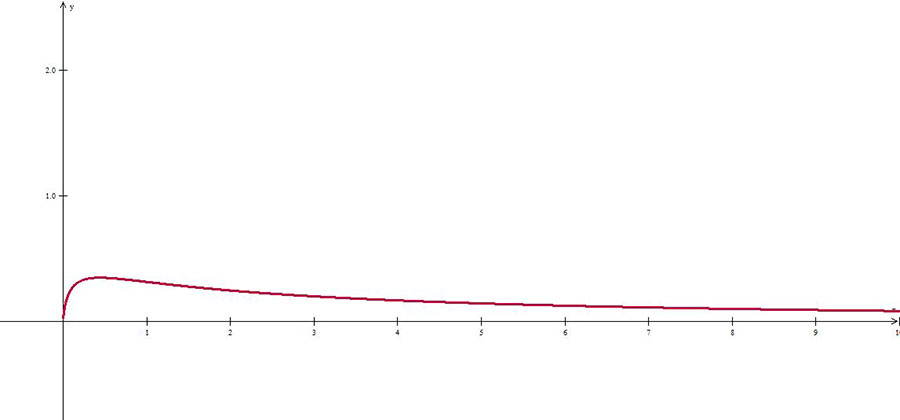
Problema: el desplazamiento de un objeto
Un poco de historia
La integración es un concepto muy aplicado en las matemáticas avanzadas, en campos como el cálculo y el análisis numérico. En el cálculo integral que es una de las ramas de las matemáticas, el proceso de integración o antiderivación es muy común en las ingenierías y se utiliza principalmente para el cálculo de áreas, volúmenes de regiones y sólidos de revolución.
Asimismo, su uso se remonta desde los inicios de la humanidad con el cálculo de las áreas de los terrenos para el cultivo de los granos.
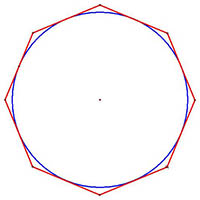
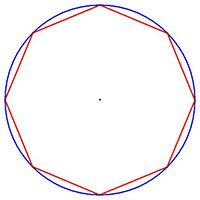
Arquímedes fue uno de los primeros matemáticos en demostrar que el área de un círculo era menor que el área del polígono circunscrito y mayor que el área del polígono inscrito, utilizando el método de exhausción propuesto por Eudoxo. El matemático determinó que cuando el número de lados del polígono de igual radio era un número muy grande, las áreas de ambos polígonos eran prácticamente iguales. Arquímedes también utilizó este método de los polígonos crecientes y decrecientes para demostrar que $\pi $ era menor que $3\frac{1}{7}$ y mayor que $3\frac{10}{71}$.
 |
 |
Polígono circunscrito. |
Polígono inscrito. |
Cálculo de áreas
El cálculo de áreas es uno de los problemas más frecuentes en matemática. Por ejemplo, considere el área $A$ bajo la curva de $f$ de la figura adjunta, donde $f \left(x \right)$ y los límites inferior y superior (a y b) son valores conocidos.
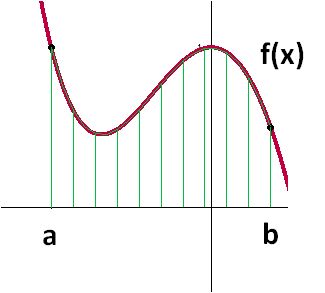
En la solución de este tipo de problemas se pueden obtener dos tipos de resultados:
- Soluciones algebraicas, en las cuales se obtiene una fórmula precisa del área solicitada.
- Soluciones numéricas, donde se hace un cálculo numérico y lo que se obtiene es una estimación del área.
Aunque estamos más habituados a las soluciones numéricas porque son exactas, lo cierto es que, en la gran mayoría de los problemas donde se necesite calcular un área, el cálculo de estas integrales por los métodos analíticos es prácticamente imposible, por lo que debemos recurrir a la integración numérica.
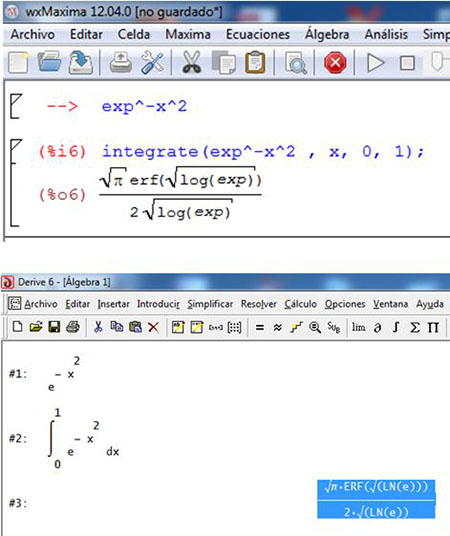
Por ejemplo, la integral $\int_{0}^{1} {e^{-x^2}} dx$ es de mucha utilidad en probabilidad y física, se puede calcular mediante integración numérica, obteniendo una buena estimación. El cálculo de la integral anterior se hizo en Maxima y en Derive como se muestra en la siguiente figura.
Problema de ambientación
Un cuerpo se desplaza linealmente a partir de cero (observar la gráfica adjunta), con una fuerza variable dada por: $f\left( x \right) = \frac{{10x}}{{{{\left( {\sqrt x + 1} \right)}^5}}}$. Donde $f$ se mide en newtons y $x$ brinda la posición del objeto en metros. Calcule el trabajo realizado por el cuerpo en un desplazamiento de 1 hasta 2 metros. Utilice los siguientes métodos:
- La regla del trapecio usando 6 nodos.
- Regla de Simpson 1/3.
- regla de Simpson 3/8.
Compare los resultados obtenidos.