Resolución del problema
Un agricultor tiene un problema en la producción de tomate, ya que una plaga ataca el cultivo. Un grupo de agrónomos y matemáticos determina que la plaga se duplicará aproximadamente entre uno o dos días. El modelo matemático encontrado, para determinar con precisión dicho tiempo, consiste en resolver la ecuación ${e^x} - {x^4} + 1 = 0$ en el intervalo $\left[ {1,2} \right]$ con una precisión de $ \in = {10^{ - 3}}$.
La imagen de la gráfica construida con el software Winplot, explicado detalladamente en el módulo 1 de este multimedia, representa la situación planteada:
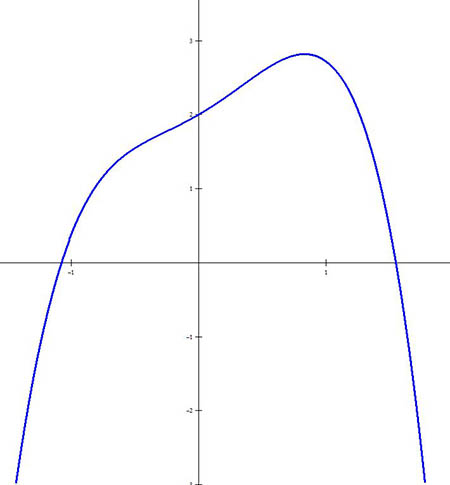
Como la plaga se duplicará aproximadamente entre uno o dos días se construye la gráfica de la función pero en el intervalo $\left[ {1,2} \right]$, como se muestra en la siguiente imagen:
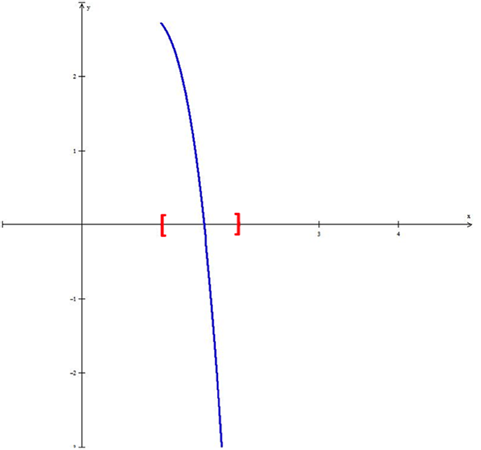
Para determinar el número de iteraciones que se requieren para calcular la raíz con la estimación pedida, se tiene que hacer uso de la fórmula ${{b - a} \over {{2^n}}} < \varepsilon $.
${{2 - 1} \over {{2^n}}} < {10^{ - 3}} \Rightarrow {1 \over {{2^n}}} < {10^{ - 3}} \Rightarrow {1 \over {{{10}^{ - 3}}}} < {2^n} \Rightarrow log{10^3} < nlog2 \Rightarrow {3 \over {log2}} < 9.96$, por lo tanto serán necesarias 10 iteraciones para obtener la raíz con un error menor a ${10^{ - 3}}$.
Como la función cumple con las condiciones para aplicar el método de bisección, entonces se tiene que:
-
La función $f$ es continua en el intervalo dado.
-
Presenta signos opuestos, pues $f\left( 1 \right) = 2.71828$
$f\left( 2 \right) = - 7.6109$, por lo tanto cumple con las condiciones para aplicar el método.
-
El punto medio de $\left[ {1,2} \right]$ es: ${{1 + 2} \over 2} = 1.5 = {p_1}$
-
$\left( {1.5} \right) = 0.4191$
-
Como $f\left( {1.5} \right)f\left( 2 \right) < 0$, entonces la raíz está en $\left[ {1.5,{\rm{ }}2} \right]$, así:
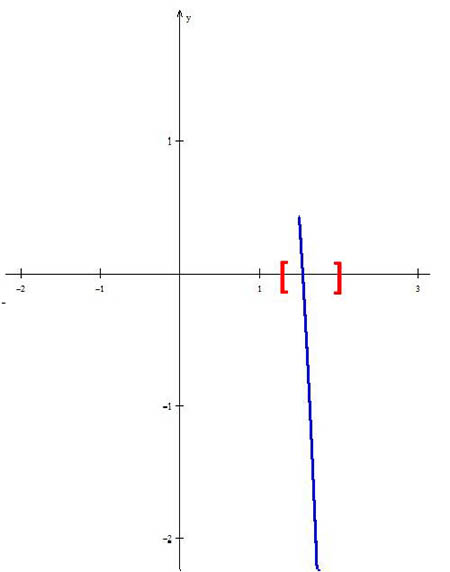
Se continúa con el proceso y se tiene que:
-
El punto medio de $\left[ {1.5,{\rm{ }}2} \right]$ es ${{1.5 + 2} \over 2} = 1.75 = {p_2}$
-
$f\left( {1.75} \right) = - 2.6243$
-
$f\left( {1.5} \right) = 0.4191$
-
Como $f\left( {1.5} \right)f\left( {1.75} \right) < 0$, entonces la raíz se encuentra en $\left[ {1.5,{\rm{ }}1.75} \right]$, según se muestra en la imagen:
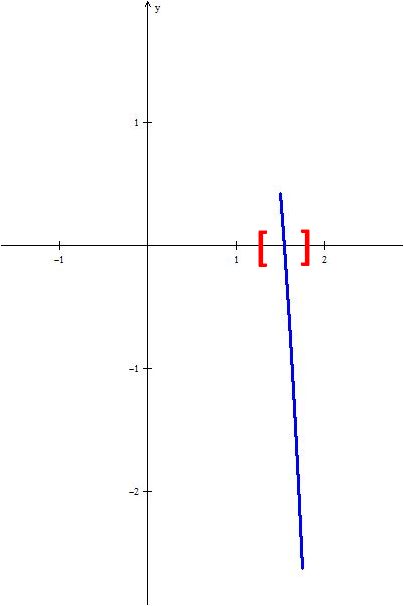
Se continúa nuevamente con el proceso y se tiene que:
-
El punto medio de $\left[ {1.5,{\rm{ }}1.75} \right]$ es:${{1.5 + 1.75} \over 2} = 1.625 = {p_3}$
-
$f\left( {1.625} \right) = - 0.8944$
-
$f(1.5) = 0.4191$
-
Como $f\left( {1.5} \right)f\left( {1.625} \right) < 0$, entonces la raíz se encuentra en el intervalo $\left[ {1.5,{\rm{ }}1.625} \right]$, como se muestra en la siguiente imagen.
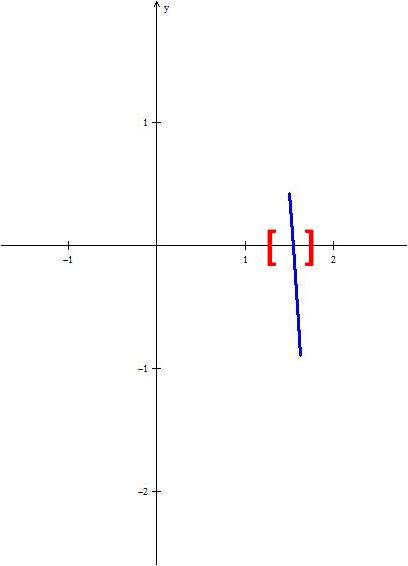
Se continúa el proceso hasta la iteración 10. En la siguiente tabla se muestran las diez iteraciones.
| Iteración | ${a_i}$ | ${b_i}$ | ${p_i} = {{{a_i} + {b_i}} \over 2}$ | $f({a_i})$ | $f({b_i})$ | $f({p_i})$ |
| 1 | 1 | 2 | 1.5 | 2.7182 | -7.6109 | 0.4191 |
| 2 | 1.5 | 2 | 1.75 | 0.4191 | -7.6109 | -2.6243 |
| 3 | 1.5 | 1.75 | 1.625 | 0.4191 | -2.6243 | -0.8944 |
| 4 | 1.5 | 1.625 | 1.5625 | 0.4191 | -0.8944 | -0.1897 |
| 5 | 1.5 | 1.5625 | 1.5312 | 0.4191 | -0.1897 | 0.1262 |
| 6 | 1.5312 | 1.5625 | 1.5468 | 0.1262 | -0.1897 | -0.0288 |
| 7 | 1.5312 | 1.5468 | 1.5390 | 0.1262 | -2.0288 | 0.0494 |
| 8 | 1.5390 | 1.5468 | 1.5429 | 0.0494 | -2.0288 | 0.0104 |
| 9 | 1.5429 | 1.5468 | 1.5449 | 0.0104 | -2.0288 | -0.0091 |
| 10 | 1.5429 | 1.5449 | 1.5439 | 0.0104 | -2.0089 | 0.0006 |
La raíz es aproximadamente 1.5439, como se muestra en la siguiente imagen.
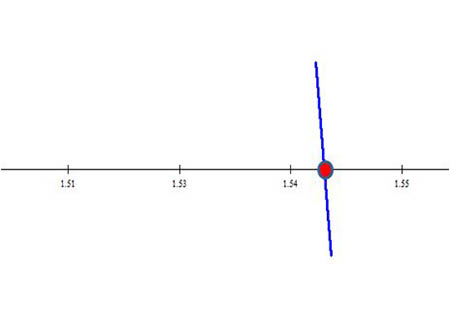
De manera, que el equipo de agrónomos, agricultores y matemáticos tendrán que tomar acciones el mismo día para que la plaga no ocasione daños graves, ya que en aproximadamente 37 horas (1.5439) se duplica la plaga en el cultivo.
Anterior: Descripción del método