Propuesta metodológica para ser implementada en secundaria
Cálculo de las raíces de la ecuación ${x^2} - 3 = 0$
Con los nuevos programas de estudio en Matemática, el estudiante que ingresa al tercer ciclo de la educación secundaria costarricense tiene que tener la habilidad de comparar y operar tanto los números naturales como los expresados en notación decimal. En este ciclo se considera de suma importancia la conceptualización y operatoria de los números enteros, racionales, irracionales y reales, ya que el área de los números está conectada con otras áreas matemáticas como: medidas, relaciones y álgebra, estadística y probabilidad.
Con esta propuesta, se pretende que el futuro docente sugiera a sus alumnos estrategias de aprendizaje donde se apliquen los números irracionales en el cálculo operatorio, así como en la resolución de problemas de su entorno local e internacional.
Es importante que en secundaria el estudiante comprenda que cuando se operan expresiones como $\sqrt 2$, $^3\sqrt 5 $, $\sqrt {{3^2} + {7^2}} $ con números decimales, se hacen mediante aproximaciones, así mismo cuando se asume $\pi $ como 3,14.
Con el método de bisección, el estudiante podrá visualizar lo señalado anteriormente y concluir que los resultados obtenidos cuando se operan con este tipo de números, son tan solo estimaciones.
Conocimientos previos
-
Resolución de ecuaciones de segundo grado.
-
Función cuadrática.
Objetivo
-
Determinar en forma aproximada, con un error de ${10^{ - 2}}$, la raíz de la ecuación ${x^2} - 3 = 0$ en el intervalo$\left[ {1,2} \right]$.
Contenidos
-
Números irracionales.
Actividades
Basados en la ecuación ${x^2} - 3 = 0$, se pregunta a los estudiantes cuáles números reales del intervalo $\left[ {1,2} \right]$ hacen verdadera la igualdad. Para ello, pídales que construyan una tabla de valores como la que se muestra a continuación:
| $x$ | ${x^2} - \sqrt 3 $ |
| 1 | -0.73205 |
| 1.01 | -0,71195 |
| 1.001 | -0.73004 |
| 1.21 | -0.26795 |
| 1.3 | -0.04205 |
| 1.7 | -0.03205 |
| . | |
| . | |
| . | |
| 2 | 2.267949 |
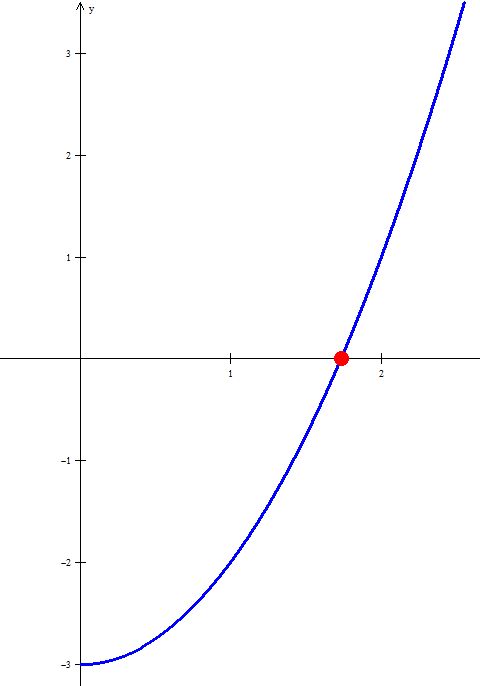
Luego, solicite que construyan la gráfica de $f\left( x \right) = {x^2} - 3$ en el intervalo $\left[ {0,{\rm{ }}3} \right]$, ya sea con papel milimétrico o con un software graficador. Para realizar esta graficación deben utilizar los contenidos de la función cuadrática. La gráfica de la función está construida en Winplot:
También, pídales que, de acuerdo con la gráfica, analicen si los números reales de la anterior tabla de valores se acercan a la raíz buscada. Puede hacer preguntas como: ¿cuál valor es exacto?, ¿existirán otros valores?, ¿se podrá determinar en forma exacta el valor de la raíz?
Para corroborar los resultados obtenidos, los alumnos aplican el método de bisección y como el error solicitado es de ${10^{ - 2}}$, tendrán que realizar 7 iteraciones. En esta actividad, pueden utilizar la calculadora científica, programable o la hoja electrónica Excel.
Comente la importancia de los métodos numéricos en la solución de ecuaciones de una variable, cuyas raíces son números irracionales.
Evaluación
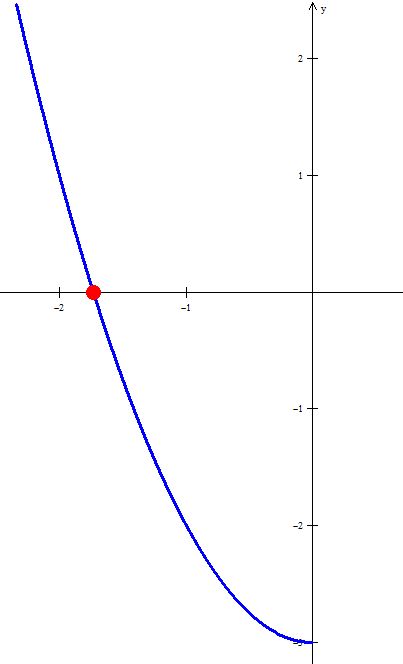
Repita la actividad para determinar la raíz de ${x^2} - 3 = 0$ pero en el intervalo $\left[ { - 2, - 1} \right]$ y pida a los estudiantes que comparen los resultados con los obtenidos en la actividad anterior. Propicie el debate de ideas para obtener una conclusión general de la actividad. La gráfica de la función en el intervalo $\left[ { - 2, - 1} \right]$ fue construida en Winplot y se muestra en la siguiente imagen.
Además, solicite a los estudiantes que calculen, en forma aproximada, el valor de $\sqrt 7 $ y que determinen una ecuación de segundo grado cuya solución sea dicho número.
Luego, pídales que presenten problemas de aplicación sobre el medio ambiente donde se haga uso del método de bisección. Para realizar esta actividad, pueden investigar en Internet, en las fábricas de su comunidad, con los líderes comunales, con los profesores de Física, Química o Biología, entre otros.