Descripción del método
Método de bisección (Bolzano)
El método de bisección es uno de los más versátiles para determinar una raíz real en un intervalo de una ecuación dada, es fácil de comprender, aunque si se desea una mayor exactitud el número de cálculos que hay que realizar aumenta considerablemente.
Una de sus ventajas es que funciona para ecuaciones algebraicas y trascendentes, pero se recomienda utilizarlo después de un análisis gráfico.
El Teorema de Bolzano establece las condiciones necesarias para la existencia de al menos un cero de una función continua.
Teorema de Bolzano
Si $f\left( x \right)$ es continua en el intervalo $\left[ {a,b} \right]$, con $f\left( a \right) \bullet f\left( b \right) < 0$, entonces existe al menos un $c \in \left] {a,b} \right[$ tal que $f\left( c \right) = 0$
El método de bisección se basa en el Teorema de Bolzano, el cual afirma que si se tiene una función real $y = f(x)$ continua en el intervalo $\left] {a,b} \right[$ donde el signo de la función en el extremo $a$ es distinto al signo de la función en el extremo $b$ del intervalo, entonces existe al menos un $c \in \left] {a,b} \right[$ tal que $f\left( c \right) = 0$, que es la raíz buscada, como se muestra en la imagen construida en Winplot.
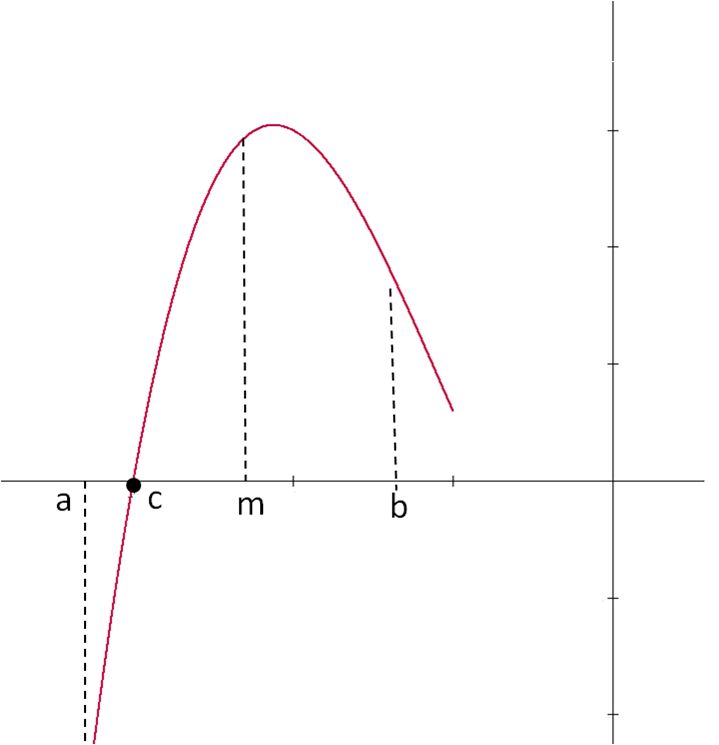
- Suponga una ecuación $f\left( x \right) = 0$
- Para determinar la raíz en el intervalo $\left] {a,b} \right[$ divida el intervalo por la mitad, llame con $m$ a ese punto donde $m = {{a + b} \over 2}$.
- Considere los siguientes casos:
-
Si $f\left( m \right) = 0$, entonces $m$ es la raíz buscada
-
Si $f\left( a \right)$ y $f\left( m \right)$ tienen signos diferentes, entonces la raíz buscada se encuentra en el intervalo $\left] {a,m} \right[$
-
Si $f\left( m \right)$ y $f\left( b \right)$ tienen signos diferentes, entonces la raíz buscada se encuentra en el intervalo$\left] {m,b} \right[$
-
Ahora, divida por la mitad el nuevo intervalo que contiene la raíz y repita el procedimiento.
-
Al continuar con el proceso, determinamos que la raíz se encuentra en un intervalo tan pequeño como se desee y, entonces, se obtiene una aproximación de la raíz buscada.
-
Observe que se va obteniendo una secuencia de intervalos cada vez más pequeños $\left] {{a_1},{b_1}} \right[, \left] {{a_2},{b_2}} \right[, \left] {{a_3},{b_3}} \right[, ..., \left] {{a_n},{b_n}} \right[,$ tal que $f\left( {{a_n}} \right) \bullet f\left( {{b_n}} \right) \to 0$, entonces ${b_n} - {a_n} = {1 \over {{2^n}}}\left( {b - a} \right)$.
-
Los puntos extremos ${a_1}, {a_2}, {a_3}, ..., {a_n}$ forman una sucesión creciente y acotada, mientras que los puntos extremos ${b_1}, {b_2}, {b_3}, ..., {b_n}$ una sucesión decreciente y acotada, con un límite común igual 𝜀 que es la raíz buscada.
-
El proceso puede ser continuado hasta lograr que $\left| {{b_n} - \left. {{a_n}} \right|} \right. < \in $, para un valor $ \in $ establecido. Este procedimiento brinda la precisión requerida para la raíz buscada.
-
Para determinar el error mínimo esperado del método, haga uso del siguiente teorema:
Teorema Cota de error para el método de bisección
Sea $f\left( x \right)$ una función continua en el intervalo $\left[ {a,b} \right]$, tal que $f\left( a \right) \bullet f\left( b \right) < 0$, entonces el método de bisección genera una sucesión $\left\{ p_n \right\}$ convergente a una raíz $p$ tal que $\left| {p_n} - {p} \right| \leq {{b - a} \over {{2^n}}}$, $n \geq 1$
- Para determinar el número máximo de iteraciones aplique la siguiente fórmula: $${{b - a} \over {{2^n}}} < \varepsilon $$
Ventajas y desventajas del Método de Bisección
Ventajas |
Desventajas |
| Es siempre convergente. | Converge muy lentamente. |
| Es óptimo para resolver una ecuación $f\left( x \right) = 0$ cuando no se sabe nada de $f$, excepto calcular su signo. | Permite encontrar solo una raíz, aunque existan más en el intervalo. |
| Requiere que $f$ sea continua en el intervalo especificado. | Algunas veces la determinación del intervalo inicial no es muy fácil. |
| Se basa en el Teorema de Bolzano. | A veces, no es obvio el criterio de finalización del proceso iteractivo. |
| Se puede establecer el límite de error. | No puede determinar raíces complejas. |
| Es fácil de implementar. | Es difícil generalizarlo para dimensiones superiores. |