Propuesta metodológica para ser implementada en secundaria
Una introducción del número irracional $\sqrt 2 $
En el estudio del concepto del número irracional en educación secundaria es importante que el estudiante conjeture, realice construcciones, cálculos y aproximaciones. Todo ello facilitará que se apropie de la noción y que logre establecer la diferencia con el número racional.
Inicialmente, para acercarse a la aproximación de $\sqrt 2 $ se podría realizar una construcción en la recta numérica de la siguiente forma:
Trace un triángulo rectángulo isósceles de una unidad de medida en cada uno de sus catetos, de manera que el vértice del ángulo recto tenga correspondencia con el número cero, tal como se muestra a continuación:
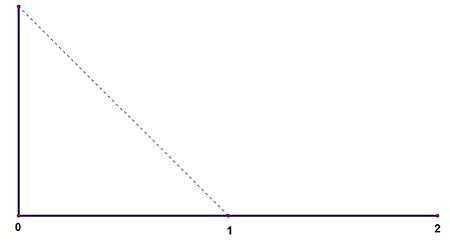
Después de trazar la hipotenusa del triángulo, mostrada en la línea punteada y de llegar a la conclusión de que ${x^2} = 2$; indique a los estudiantes que el valor de 
de signo positivo que hace correcta la igualdad, recibe el nombre de raíz cuadrada de dos y se escribe $\sqrt 2 $.
Luego, transporte esta distancia a la recta con un compás, como se muestra seguidamente:
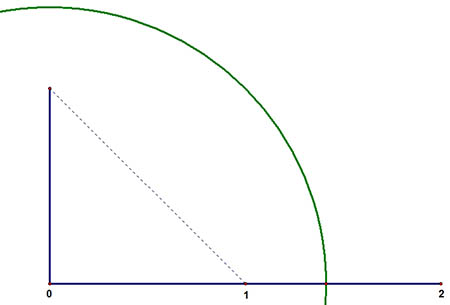
Solicite a los estudiantes que midan la distancia desde 0 hasta la intersección de la circunferencia con la recta numérica y que anoten los resultados. Posiblemente, algunos anotarán 1,4 y otros 1,5. Es importante manifestarles que solo debe haber una aproximación del número.
Seguidamente, pueden efectuar el cálculo:
$ {\left( {1.4} \right)^2} = 1.4 \bullet 1.4 = 1.96 $
$ {\left( {1.5} \right)^2} = 1.5 \bullet 1.5 = 2.25 $
Este paso permite corroborar que los estudiantes que midieron 1,4 se acercaron más a $\sqrt 2 $, pues 1,96 está más cerca de 2 que 2,25.
Después, solicíteles que construyan una tabla para aproximarse más a $\sqrt 2 $. La idea es que multipliquen y se aproximen al valor por ensayo y error. Una muestra de la posible tabla construida por los estudiantes es la siguiente:
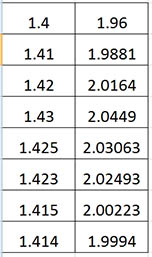
Después, coménteles que la aproximación del número $\sqrt 2 $ que proporciona el software Maxima, con 15 decimales, es 1,414213562373095 pero que su expansión decimal es infinita y no periódica, por lo cual se diferencia de un número racional.
Ahora, invítelos a que determinen el error absoluto de la primera aproximación y explique porqué la fórmula lleva valor absoluto. Se podría aprovechar la experiencia de la actividad anterior, en la cual algunos estudiantes asignaron valores mayores y otros valores menores, para realizar esta explicación, por ejemplo en estos dos casos:
$$\left| {1.4 - {\rm{1}}{\rm{.414213 562373095}}} \right| = \left| {{\rm{ - 0}}{\rm{.014213562373095}}} \right| = {\rm{0}}{\rm{.01421356237309}}$$
$$\left| {1.5 - {\rm{1}}{\rm{.414213 562373095}}} \right| = \left| {{\rm{0}}{\rm{.085786437626905}}} \right| = {\rm{0}}{\rm{.085786437626905}}$$
En este momento, se puede comunicar al estudiante la importancia del error y, también, explicar que si se requiere mayor precisión tendría que utilizar mejores instrumentos, recursos y software para disminuir dicho error.
Puede plantear problemas como el que se presenta en este módulo, adecuándolos tanto al contexto como al nivel, con una apropiada transposición didáctica. Es importante que el estudiante entienda que con los números decimales se pueden realizar buenas aproximaciones de los números irracionales, aunque nunca se conocerá el valor real.
Evaluación
Solicite a sus estudiantes que consideren la fracción ${{41} \over {29}}$ y que la expresen en forma decimal. A partir de esta expresión, se puede generar una situación de aprendizaje que le permita evaluar los conceptos estudiados. Serán fundamentales preguntas como las siguientes.
- ¿Es ${{41} \over {29}}$ un número irracional?
- ¿Es equivalente a $\sqrt 2 $?
- ¿Es una aproximación de $\sqrt 2 $?
- ¿Cuál es el error de aproximar a $\sqrt 2 $ utilizando ${{41} \over {29}}$ ?
Además, invítelos a investigar otra fracción que se aproxime mejor a $\sqrt 2 $, pueda que se presenten respuestas como ${{239} \over {169}}$.
Finalmente, les puede solicitar que busquen referencias históricas importantes, como por ejemplo: los pitagóricos y los números irracionales.