Tutorial para la resolución de a y b
Resolución de a: cálculo de la aproximación en punto flotante
Para resolver el cálculo de la aproximación en punto flotante se utilizará el software Maxima. Primero debe tener el programa instalado en su computadora para poder ejecutarlo; si todavía no lo ha instalado puede hacerlo siguendo la guía correspondiente en este material.
Además, tome en cuenta algunas aclaraciones:
-
En Maxima, la región en blanco es para digitar las expresiones matemáticas y los distintos menús permiten realizar varios cálculos.
-
Para digitar la expresión matemática que modela el recorrido del proyecto, primero se oprime Enter y, después, se digita la ecuación.
-
En Maxima se utiliza el signo de punto para indicar la separación de los números enteros de los decimales, contrario a lo que dicta el Sistema Internacional de Pesos y Medidas, que recomienda el uso de la coma.
1. Tenga en cuenta que debe utilizar un asterisco (*) para indicar multiplicación, sino Maxima no reconocerá la operación. Cuando termine de digitar, presione las teclas Shift y Enter simultáneamente para verificar. En la siguiente figura se muestra tanto lo digitado como la salida con Maxima:
Observe, se igualó la ecuación a 0 porque es necesario que el proyectil se encuentre en el suelo. Además, uno de los coeficientes de la ecuación es procesado en forma distinta, pero esto no afecta los resultados.
2. Para resolver esta ecuación se tiene que $a=-2.1$, $b=8.5$ y $c=1.8$, previamente se utilizó la fórmula general $x = {{ - b \pm \sqrt {{b^2} - 4ac} } \over {2a}}$ que es usada para resolver ecuaciones de segundo grado. En Maxima se debe ubicar el número de decimales con los cuales se trabajará por medio de la instrucción fpprec, tal como se muestra en la siguiente imagen:
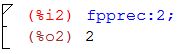
3. El primer cálculo que se realizará es $4ac$, o sea: $\left( {0.4{\rm{ }}x{\rm{ }}{{10}^1}} \right){\rm{ }}x{\rm{ }}\left( { - 0.21{\rm{ }}x{\rm{ }}{{10}^1}} \right){\rm{ }}x{\rm{ }}\left( {0.18{\rm{ }}x{\rm{ }}{{10}^1}} \right)$. La instrucción para que Maxima proporcione el resultado en punto flotante con dos decimales es bfloat, vea la siguiente imagen:
El resultado que proporciona el software es $ - 1.5b1$, o sea, $ - 1.5{\rm{ }}x{\rm{ }}{10^1}$, la $b$ se utiliza para la potencia de base 10, con 1 como su exponente, si lo escribimos en notación punto flotante, como se describe en la unidad didáctica, sería: $ - 0.15{\rm{ }}x{\rm{ }}{10^2}$.
4. Se calculan a continuación ${b^2}$, ${b^2} - 4ac$, $\sqrt {{b^2} - 4ac} $, $ - b - \sqrt {{b^2} - 4ac} $, ${{ - b - \sqrt {{b^2} - 4ac} } \over {2a}}$.
- Expresión matemática: ${b^2}$
Instrucciones y resultado en Maxima:
En notación punto flotante: ${0.72x{{10}^2}}$
- Expresión matemática: ${b^2} - 4ac$
Instrucciones y resultado en Maxima:
En notación punto flotante: ${0.87x{{10}^2}}$
- Expresión matemática: $\sqrt {{b^2} - 4ac} $
Instrucciones y resultado en Maxima:
En notación punto flotante: ${0.93x{{10}^1}}$
- Expresión matemática: $ - b - \sqrt {{b^2} - 4ac} $
Instrucciones y resultado en Maxima:
En notación punto flotante: ${ - 0.18x{{10}^2}}$
- Expresión matemática: ${{ - b - \sqrt {{b^2} - 4ac} } \over {2a}}$
Instrucciones y resultado en Maxima:
En notación punto flotante: ${0.43x{{10}^1}}$
El tiempo calculado en punto flotante con dos dígitos y redondeo es ${0.43x{{10}^1}}$. Dicho de otra manera, aproximadamente 4,3 horas que equivalen a 4 horas y 18 minutos.
El desarrollo en forma continua del ejercicio, sin comentarios, se expone a continuación:
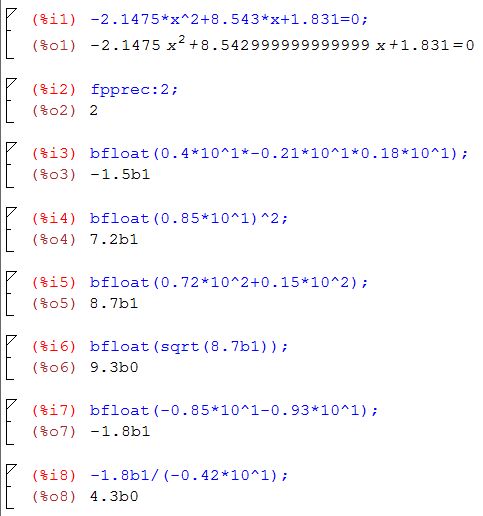
Cuando el estudiante adquiera más destrezas en Maxima podrá realizar los cálculos haciendo referencia a procesos anteriores, por ejemplo en el paso seis se requiere calcular la raíz cuadrada del resultado cinco, esto lo puede hacer escribiendo la misma simbología del resultado cinco, en este caso (%o5), como se ilustra a continuación:
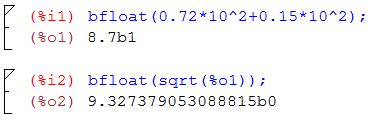
En este caso se mostraron los quince decimales que trae definido por defecto el software, debido a que no se definió la precisión.
Resolución de b: cálculo del error asociado a la aproximación anterior
Para calcular el error asociado, primero seleccione la ecuación; luego, en el menú Ecuación marque la opción Resolver, así:
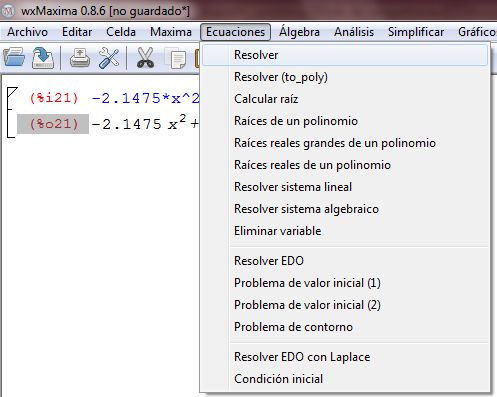
Después, en la caja de diálogo, presione el botón Aceptar, para que se desplieguen ambas soluciones, vea la siguiente figura:
Si desea conocer la aproximación de la solución, seleccione uno de los resultados de x y luego seleccione la opción A Real en el menú Numérico:
Después de ejecutar el paso anterior, se desplegará la aproximación de la solución:
Maxima presenta las aproximaciones con 15 decimales o con 16 en punto flotante, si desea una mayor aproximación tendría que utilizar la instrucción fpprec, tal como se realizó anteriormente.
A continuación, se muestran los procedimientos para encontrar: el error absoluto, el error relativo y el error relativo porcentual:
Error absoluto
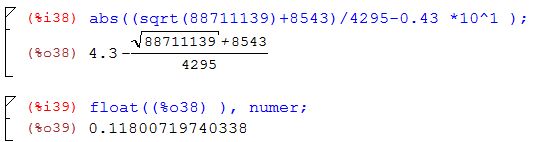
Error relativo
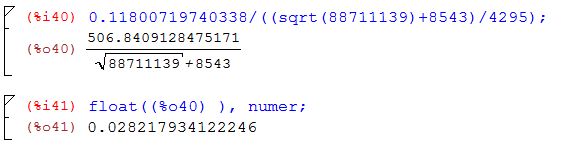
Error relativo porcentual
El error producido fue de aproximadamente 2.82%, significa que en las 4 horas y 18 minutos que tarda el proyectil los cálculos pueden fallar en 0.11 horas, unos siete minutos, tiempo que en algunos casos, como el del ejemplo, podría ser considerable.