Tutorial para la resolución de b y c
-
Cálculo de la solución utilizando una interpolación con un modelo cuadrático
- Sean los puntos $A(5,12)$, $B(9,18)$ y $C(13,28)$, con los que se construirá una función cuadrática. La forma general de una ecuación cuadrática es $f(x) = a{x^2} + bx + c$, con $a,b,c \in {\Cal R}$, $a \ne 0$. Como los puntos dados pertenecen a la función cuadrática, entonces se tiene que $f(5) = 12$, $f(9) = 18$ y $f(13) = 28$.
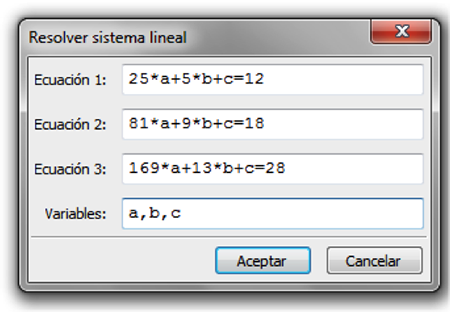
- Con base a lo anterior, se forma un sistema de tres ecuaciones lineales con tres incógnitas: $$\eqalign{ & 25a + 5b + c = 12 \cr & 81a + 9b + c = 18 \cr & 169a + 13b + c = 28 \cr} $$
-
El sistema de ecuaciones se puede resolver utilizando Maxima; acceda a la opción Resolver sistema lineal del menú Ecuaciones, tal como se muestra en la siguiente figura:
-
Después, el software muestra una caja de diálogo que solicita el número de ecuaciones con las que se va a trabajar, 3 en este caso:
-
Una vez que se oprimió el botón Aceptar, se pueden ingresar las tres ecuaciones:
-
Luego, el software proporciona el valor de las constantes $a,b,c$; de la siguiente manera:

- Basándose en estas constantes, se concluye que la función cuadrática que contiene los pares ordenados es $f(x) = \frac{1}{8}{x^2} + \frac{1}{4}x + \frac{{81}}{8}$. Con este criterio se pueden calcular las aproximaciones para 7 millones y para 10 millones, que es lo que requiere la compañía.
- Para obtener las aproximaciones, oprima Enter sobre la hoja de trabajo y, en el espacio que se abre para escribir, digite la ecuación anterior; cuando finalice, presione simultáneamente Shift y Enter. Se obtiene el siguiente resultado:
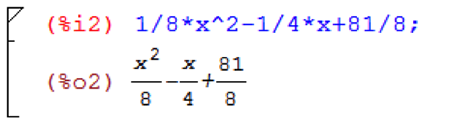
-
Para encontrar las aproximaciones, se sustituyen los valores de 7 y 10, seleccionando la ecuación con el mouse y, en la pestaña Sustituir del menú Simplificar, se cambia la $x$ por el 7, tal como se muestra a continuación:
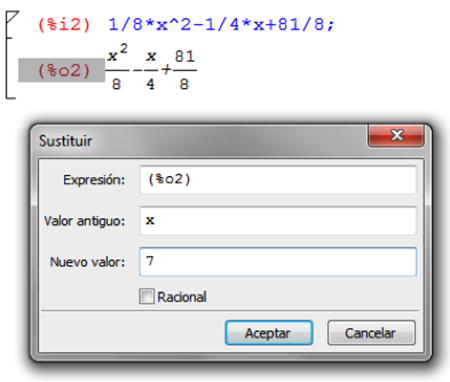
-
Seguidamente, se mostrará el resultado, en este caso $\frac{{29}}{2} = 13.5$ millones, según la siguiente figura:

- Se realiza la misma acción para 10 y se obtiene $\frac{{161}}{8} = 20.125$.
-
Para realizar la gráfica de dicha función en Winplot, escoja la pestaña Explícita del menú Ecuación, digite la ecuación $f(x) = \frac{1}{8}{x^2} - \frac{1}{4}x + \frac{{81}}{8}$, con el dominio respectivo, en este caso $\left[ {5,13} \right]$:
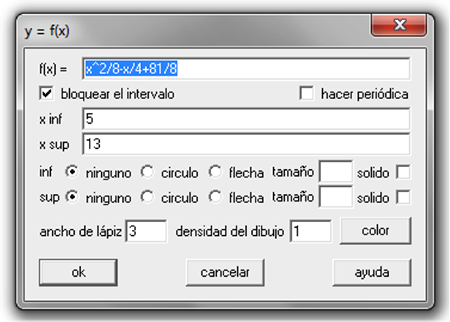
-
Después de presionar el botón Ok, no se mostrará la gráfica debido a que la zona de visualización no incluye el dominio de la función. Haga los ajustes correspondientes en el menú Ver, como se realizó en la función lineal:
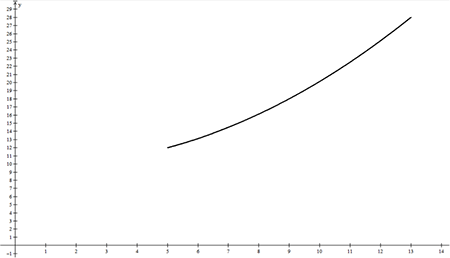
-
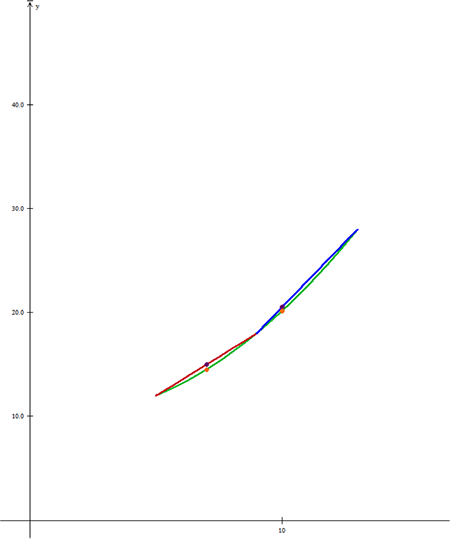
Finalmente, se modifica la escala en el eje $y$, se grafican los puntos y se obtiene una representación así:
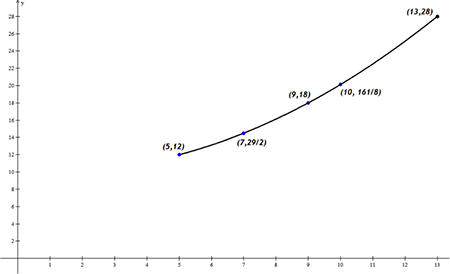
-
Consejo para la empresa
A la compañía se le recomienda que asuma un modelo para la toma de decisiones, porque deben conocer diversos aspectos como: condiciones del mercado, amenazas y riesgos del entorno, economía del país, economía internacional, entre otros. Después, la compañía podrá valorar cuál de los dos modelos es más apropiado o si le conviene adoptar otro. Depende de lo que la empresa quiera, las diferencias que se presentan en los dos modelos pueden llegar a ser muy significativas en la toma de decisiones. En la siguiente tabla, se resumen los resultados obtenidos con ambos modelos:
Modelo |
Gastos |
Ingresos |
Lineal |
7 millones |
15 millones |
10 millones |
20.5 millones |
|
Cuadrático |
7 millones |
14.5 millones |
10 millones |
20.125 millones |
En la siguiente figura se muestran las gráficas generadas por ambos modelos, observe la ubicación de los puntos.