Propuesta metodológica
Interpolación, física y función lineal
La interpolación se puede relacionar con los conceptos de proporción y función lineal.
Considere el siguiente problema: un auto realiza el recorrido de 400 km, entre San José y Ciudad Neilly, como se muestra en la siguiente figura:
Los tiempos y las distancias del auto se resumen en la siguiente tabla:
$t$ (hrs) |
1 |
4 |
5 |
8 |
$d$ (k/m) |
50 |
200 |
250 |
400 |
Con base en la tabla anterior, el docente puede plantear a sus estudiantes las siguientes interrogantes:
- ¿Qué tipo de movimiento describe el auto?
Respecto a esta pregunta, comente que en este tipo de movimiento se cumple lo siguiente: el producto de la velocidad por el tiempo es igual a la distancia $\left( {v \bullet t = d} \right)$, esto ocurre porque la velocidad es constante en todo el recorrido y, por consiguiente, la aceleración del auto es igual a cero. Los estudiantes deben investigar por qué la aceleración es igual a cero.
-
¿Cuál es la velocidad del auto?
Como $v \bullet t = d$ entonces $v = {d \over t}$, al tomar cualquier par ordenado de la tabla se obtiene: $v = {{300} \over 6} = 50$ km por hora.
Ahora, el docente expone la existencia de una proporcionalidad directa entre la distancia y el tiempo, en este caso particular, 50 es la constante de esta proporcionalidad.
- ¿Cuántas horas tarda el auto en recorrer 320 km?
Para resolver esta interrogante se puede aplicar una interpolación lineal, de la siguiente manera:
$d = mt + b$ con $m = {{400 - 250} \over {8 - 5}} = {{150} \over 3} = 50$
Además, $250 = 50 \bullet 5 + b \Rightarrow b = 0$
Por tanto: $d = 50t$
Como $d = 320 \Rightarrow 320 = 50 \bullet t \Rightarrow t = {{320} \over {50}} = 6.4\;hrs$
Por consiguiente, el auto tardaría 6 horas y 24 minutos en recorrer los 320 km.
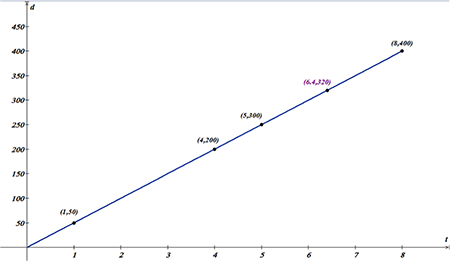
- Realice una representación gráfica del recorrido realizado.
A continuación, se muestra la gráfica del recorrido realizado por el auto, basándose en esta el docente puede preguntarles a los estudiantes:
-
¿Por qué existe una constante de proporción?
-
¿Por qué la relación es una función?
-
¿Cuáles son el dominio y el ámbito de la función?
-
¿Qué propiedades tienen las funciones que contienen el origen?
-
¿Cuál es la relación de dependencia entre la variable distancia respecto al tiempo?
Evaluación
-
El docente podría proponer otros casos que cumplan con este tipo de relación, como, por ejemplo, la relación entre el radio y la medida de la circunferencia, que también es una constante.
-
Con una tabla de valores como la siguiente:
$t$ (hrs) |
1 |
4 |
5 |
8 |
$d$ (k/m) |
60 |
210 |
260 |
410 |
Además, se puede solicitar a los estudiantes que determinen la fórmula que relaciona las dos variables y plantear la interrogante sobre la existencia de una constante de proporcionalidad en la relación dada. Finalmente, se puede invitar a que le interpolen un dato realizando la respectiva gráfica.