Métodos numéricos
T- T T+

Tutorial para la resolución de a

  1. Cálculo de la solución utilizando una interpolación con un modelo lineal

  1. Sean los puntos $A(5,12)$, $B(9,18)$ y $C(13,28)$. Primero, se construirá una función lineal que contenga los puntos $A$ y $B$, con dominio $\left[ {5,9} \right]$; posteriormente, otra que contenga los puntos $B$ y $C$, con dominio $\left] {9,13} \right]$.
  2. La ecuación de la recta corresponde a $y = mx + b$, en donde $m$ es su pendiente y se calcula con la fórmula $m = {{{y_2} - {y_1}} \over {{x_2} - {x_1}}}$. Luego, conocida $m$, se calcula $b$ sustituyendo cualquiera de los dos puntos en la ecuación ${y_n} = m{x_n} + b$, en donde $({x_n},{y_n})$ es cualquiera de los dos puntos dados.
  3. Para $A(5,12)$ y $B(9,18)$, se tiene que $m = {{18 - 12} \over {9 - 5}} = {6 \over 4} = {3 \over 2}$ y para calcular $b$ se presenta que $12 = {3 \over 2} \bullet \,5 + b \Rightarrow 12 = {{15} \over 2} + b$, entonces $12 - {{15} \over 2} = b \Rightarrow b = {9 \over 2}$. Por tanto, la ecuación de la recta que contiene a $A(5,12)$ y $B(9,18)$ tiene por ecuación $y = {3 \over 2}x + {9 \over 2}$.
  4. Para $B(9,18)$y $B(13,28)$, se tiene que $m = {{28 - 18} \over {13 - 9}} = {{10} \over 4} = {5 \over 2}$, para calcular $b$, se tiene que $18 = {5 \over 2} \bullet \,9 + b \Rightarrow 18 = {{45} \over 2} + b$, entonces $18 - {{45} \over 2} = b \Rightarrow b =  - {9 \over 2}$. Por tanto, la ecuación de la recta que contiene a $B(9,18)$ y $C(13,28)$ tiene por ecuación $y = {5 \over 2}x - {9 \over 2}$
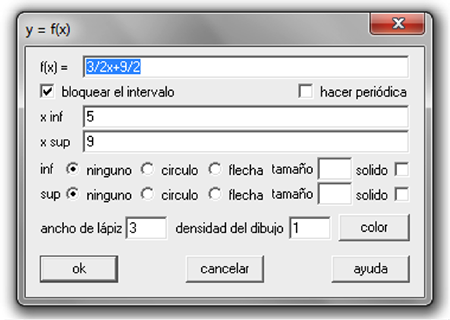
  5. Ahora, en Winplot se grafican ambas rectas. Primero, se accede a dos dimensiones (2-dim) utilizando la opción Explícita del menú Ecuación y se digita la recta  ${3 \over 2}x + {9 \over 2}$ con su respectivo dominio, tal como se muestra a continuación:
    Pantalla Winplot, menú ecuación, 2 dimensiones
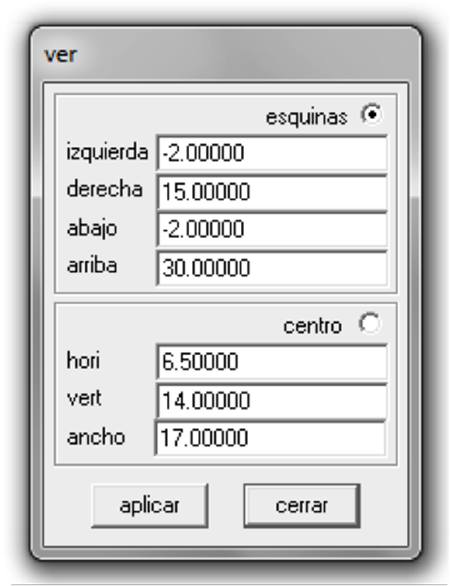
  6. Para observar la gráfica, ajuste la visualización de manera que contenga tanto el dominio como el ámbito de la función.  Observe que $y(5) = 12$ y $y(13) = 24$, por lo que se puede ajustar en $x$ desde -2 a 15, esto cubre el dominio. Además, en y desde -2 hasta 30, esto cubre el ámbito. Lo anterior se realiza seleccionando la opción Ver del menú Ver:
    Winplot, menú ver

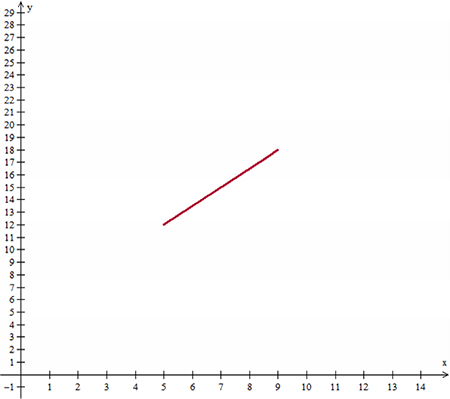
    El resultado mostrará la siguiente figura.
    Gráfica realizada en Winplot
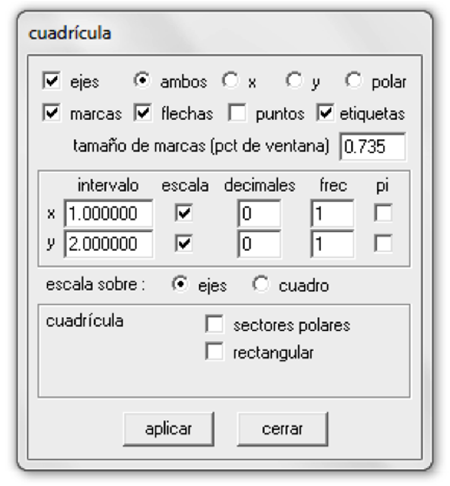
  7. Como se puede apreciar, los números en el eje $y$ quedan un poco pegados, lo cual se puede solucionar con la herramienta Cuadrícula del menú Ver, cambiando la opción del intervalo del eje $y$, para que enumere de dos en dos, tal como se muestra a continuación:
    Winplot, menú ver, herramienta cuadrícula
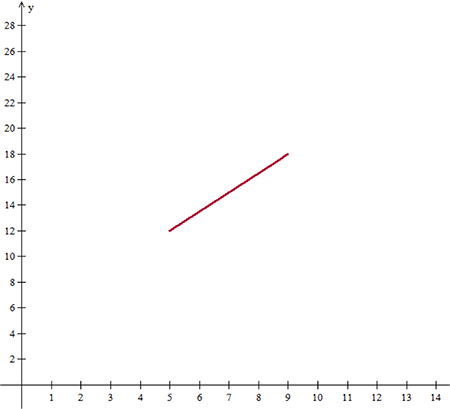
  8. El resultado obtenido será el siguiente:
    Gráfica corregida, Winplot
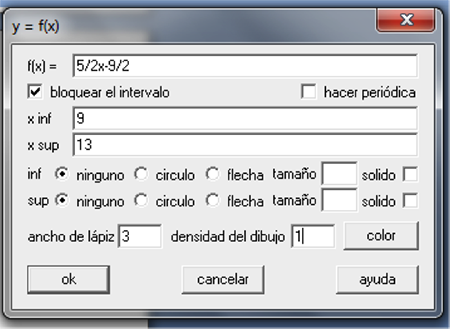
  9. Seguidamente,  se puede digitar la otra función, utilizando igualmente la opción Explícita del menú Ecuación, se escribe la función ${5 \over 2}x - {9 \over 2}$, con dominio $\left] {9,13} \right]$. El 9 se deja abierto para cumplir con la relación dada, que es una función:
    Winplot, menú ecuación, ficha explícita
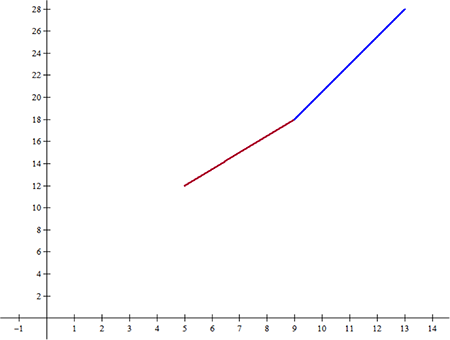
  10. El resultado de ejecutar lo anterior, se ve así:
    Gráfica Winplot
  11. Se ha encontrado un modelo lineal para la relación gasto-ingreso de la compañía YOMA S.A. Ahora, se puede utilizar el criterio de la primera función encontrada para obtener la aproximación lineal, para un gasto de 7 millones y el segundo para obtener la de 10 millones, entonces:
    $y = {3 \over 2}\left( 7 \right) + {9 \over 2} = 15$, además, $y = {5 \over 2}\left( {10} \right) - {9 \over 2} = 20.5$. Por tanto, tomando en cuenta un modelo lineal, para 7 millones de gastos la aproximación sería de 15 millones en ingresos y para 10 millones de 20.5 millones.
  12. Estos pares ordenados se pueden representar en la gráfica, utilizando la opción Punto del menú Ecuación:
    Gráfica Winplot

Anterior: Problema

Siguiente: Resolución de b y c

Arriba