1. Sumario
- Cinemática rotacional
- Momento de inercia
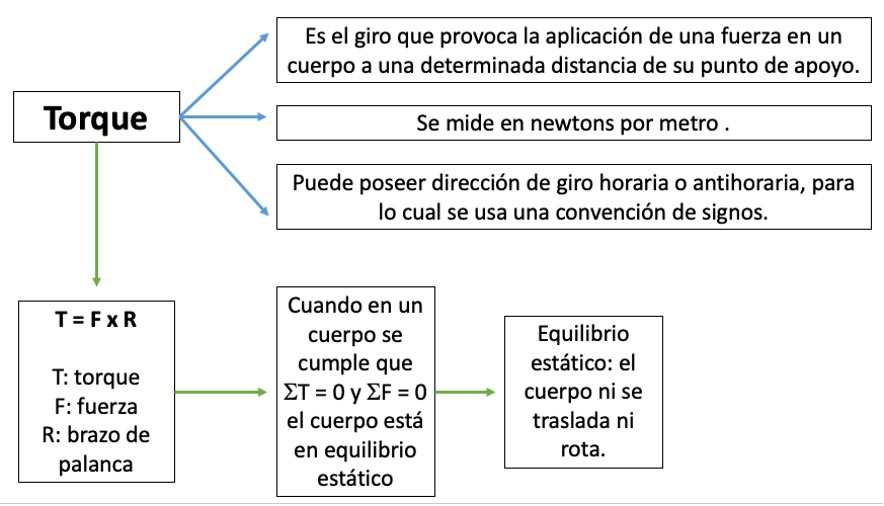
- Torque
- Dinámica rotacional
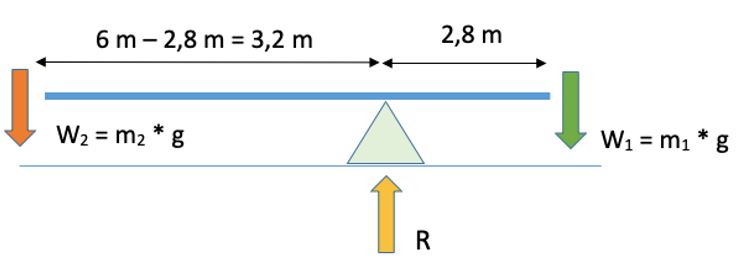
- Equilibrio estático
- Momento angular
2. Objetivo
Al finalizar el estudio de este capítulo, entre otras habilidades, usted será capaz de:
- Describir y cuantificar situaciones de movimientos de cuerpos que se encuentren rotando respecto de un eje, así como el trabajo y las energías asociadas.
3. Introducción
A continuación, se presentan una serie de sugerencias para cumplir con las experiencias de aprendizaje, que se proponen en el programa del curso de Física para Ingeniería Agroindustrial. Si bien son aplicables al curso, no son exhaustivas, por lo cual, el estudiante puede aprovechar otros materiales recomendados en las referencias bibliográficas.
4. Guía de lectura
- Debe efectuar la lectura de las secciones del libro en las cuales se trabajen los temas contenidos en el sumario. Preste particular atención a los conceptos de radián, velocidad, desplazamiento y aceleración angulares, momento de inercia, brazo de palanca y torque, energía cinética rotacional, equilibrio estático y momento angular. Puede elaborar materiales de estudio como los comentados en la sección “Consideraciones metodológicas”. Asimismo, apunte las ecuaciones más importantes para la resolución de ejercicios numéricos. Además de la lectura, se le sugiere a continuación una serie de recursos de apoyo para su estudio.
- Video sobre el movimiento circular uniformemente acelerado. Enlace: https://www.youtube.com/watch?v=05brkZpiQ2o (Duración: 3 minutos)
- Video sobre sólidos rígidos y torque. Enlace: https://www.youtube.com/watch?v=9yHnhbhTvXg (Duración: 4 minutos)
- Video sobre equilibrio estático. Enlace: https://www.youtube.com/watch?v=hDfz45XrstU (Duración: 3 minutos)
- Portal de aprendizaje sobre sólidos rígidos y rotación. Enlace: http://www2.montes.upm.es/dptos/digfa/cfisica/solido/solido_portada.html
- Espacio de experimentación con torques y equilibrio estático (simulación). Enlace: https://phet.colorado.edu/es/simulation/balancing-act
- Espacio de experimentación con torques (simulación). Enlace: https://phet.colorado.edu/es/simulation/legacy/torque
5. Comentarios del tema
6. Referencias bibliográficas
Traful, UTEM. (2016). Equilibrio de una partícula y un sólido rígido. Recuperado de: https://www.youtube.com/watch?v=hDfz45XrstU
Traful, UTEM. (2016). Movimiento circular con aceleración angular constante. Recuperado de: https://www.youtube.com/watch?v=05brkZpiQ2o
Traful, UTEM. (2016). Sólido rígido y concepto de torque. Recuperado de: https://www.youtube.com/watch?v=9yHnhbhTvXg
Universidad Politécnica de Madrid. (s.f). Sólido rígido. Recuperado de: http://www2.montes.upm.es/dptos/digfa/cfisica/solido/solido_portada.html
University of Colorado. (s.f.). Ley de equilibrio [simulación interactiva]. Recuperado de: https://phet.colorado.edu/es/simulation/balancing-act
University of Colorado. (s.f.). Torque [simulación interactiva]. Recuperado de: https://phet.colorado.edu/es/simulation/legacy/torque