Energía y trabajo

Energía y trabajo

1. Sumario

  • Trabajo
  • Energía cinética
  • Potencia
  • Energía potencial (gravitatoria y elástica)
  • Energía Mecánica
  • Conservación de la energía

2. Objetivo

Al finalizar el estudio de este capítulo, entre otras habilidades, usted será capaz de:

  • Comprender los conceptos de trabajo y energía presentes en la cotidianidad para su aplicación en la resolución de problemas en varias disciplinas.

3. Introducción

A continuación, se presentan una serie de sugerencias para cumplir con las experiencias de aprendizaje, que se proponen en el programa del curso de Física I (teoría). Si bien son aplicables al curso, no son exhaustivas, por lo cual, cada estudiante puede aprovechar otros materiales recomendados en las referencias bibliográficas.

4. Guía de lectura

  1. Debe efectuar la lectura de las secciones del libro en las cuales se trabajen los temas contenidos en el sumario. Preste particular atención a las definiciones conceptuales y matemáticas de trabajo, energía (cinética, potencial, potencial gravitatoria, potencial elástica), potencia y Teorema Energía-Trabajo. Puede elaborar materiales de estudio como los comentados en la sección “Consideraciones metodológicas”. Asimismo, apunte las ecuaciones más importantes para la resolución de ejercicios numéricos. Además de la lectura, se le sugiere a continuación una serie de recursos de apoyo para su estudio
  2. Video sobre trabajo y potencia. Enlace: https://www.youtube.com/watch?v=MZdNjS5_60I (Duración: 4 minutos)
  3. Video sobre trabajo y energía cinética. Enlace: https://www.youtube.com/watch?v=KtSjhb3EMx4 (Duración 5 minutos)
  4.  Videos sobre conservación de la energía y aplicación. Enlace: https://www.youtube.com/watch?v=jG0zDp3rZVk y https://www.youtube.com/watch?v=5Ylxn5VWm-A (Duración: 6 y 2 minutos)
  5. Espacio de experimentación con energía mecánica (simulación). Enlace: https://phet.colorado.edu/sims/html/energy-skate-park-basics/latest/energy-skate-park-basics_en.html
  6. Espacio de experimentación con energía potencial elástica (simulación). Enlace: https://phet.colorado.edu/en/simulation/masses-and-springs
  7. Video sobre aporte a Conservación de la Energía en los Principia por parte de Emilie Du Chatelet (Duración 8minutos): (9) EL Legado de la extraordinaria Émilie du Châtelet – YouTube

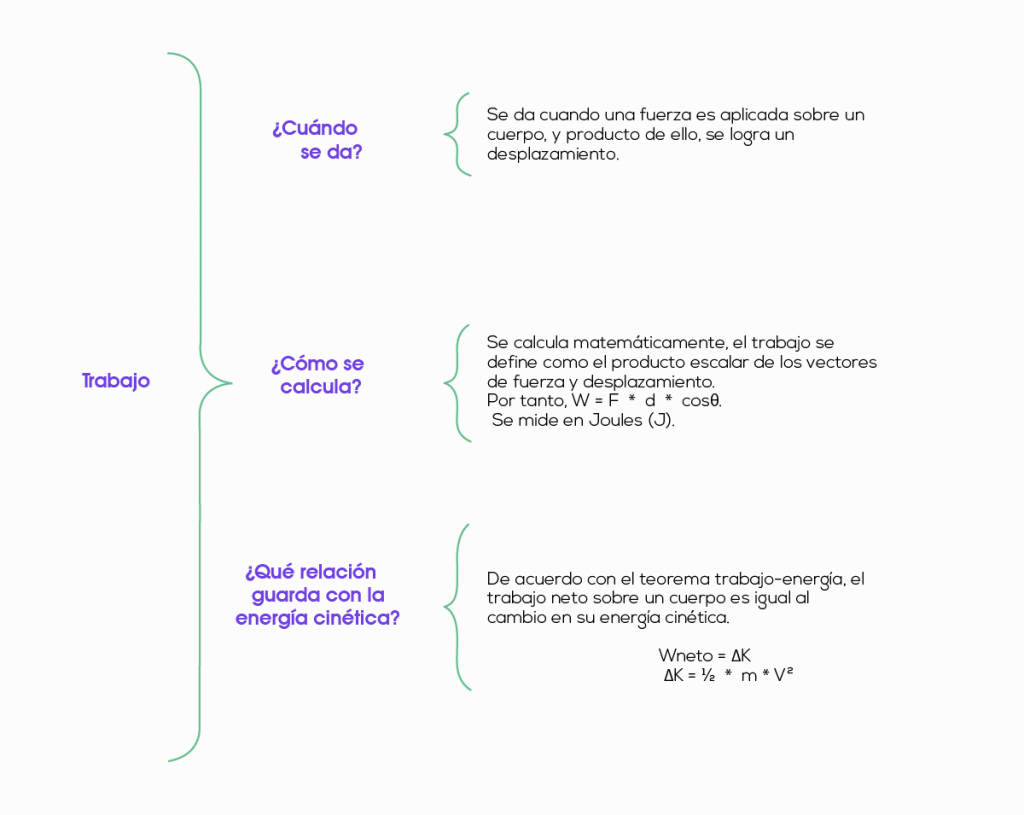
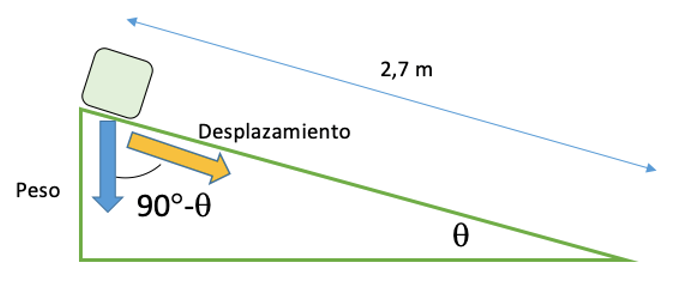
5. Esquemas y ejemplos

Cuadro sinóptico

A continuación, se le muestra un ejemplo de cuadro sinóptico sobre los temas de trabajo y energía cinética.

Ejemplo de cuadro sinóptico sobre los temas de trabajo y energía cinética
Ejercicios

A continuación, se presentan dos ejercicios resueltos, uno de trabajo y uno de conservación de la energía mecánica.

Ejercicio No. 1.  La superficie inclinada de una rampa es extremadamente lisa y posee una longitud de 2,7 m. Determine qué ángulo de inclinación debe tener la rampa para que, al colocar una caja llena con libros en su parte más elevada para que parta del reposo, llegue a la base con una rapidez de 3,4 m/s.

$$\rightarrow Peso=m\ g$$

$$\rightarrow Trabajo=Peso\ast Desplazamiento\ast Coseno\ del\ ángulo\ entre\ los\ dos$$

$$\rightarrow W=\ m\ g\ d\ cos(90° -\ θ)$$

$$\rightarrow El\ trabajo\ neto\ es\ igual\ al\ cambio\ en\ la\ energía\ cinética:$$

$$W=\ \frac{1}{2}\ m\ {V_f}^2-\frac{1}{2}\ m\ {V_i}^2$$

$$m\ g\ d\ cos(90° -\ θ)= \frac{1}{2}\ m {V_f}^2\ -\ \frac{1}{2}\ m {V_i}^2$$

$$m\ g\ d\ cos(90° -\ θ)= \frac{1}{2}\ m {V_f}^2$$

$$g\ d\ cos(90° -\ θ)= \frac{1}{2}\ {V_f}^2$$

$$g\ d\ senθ= \frac{1}{2} {V_f}^2$$

$$senθ= \frac{{V_f}^2}{2\ g\ d } $$

$$θ\ = {sin}^-1 \left(\frac{{V_f}^2}{2\ g\ d} \right)$$

$$\theta=\ \sin^{-1}{\left[\frac{\left(3,4\ m/s\right)^2}{2\ast9,8\ m/s^2\ast\ 2,7m}\right]}$$

$$\theta=12,6°$$

Ejercicio No. 2.  Un resorte cuya constante es de 1,5 kN/m está fijo en uno de sus extremos al piso. Si el resorte se comprime 7,2 cm respecto de su posición de equilibrio y se coloca en su extremo una bola de goma de 80 g ¿con qué rapidez saldrá la bola dirigida hacia arriba una vez que se despegue del resorte?

$${EM}_1=\ {EM}_2$$

$$U_{elástica1}+K_1= U_{elástica2}+K_2$$

$$U_{elástica1}= K_2$$

$$\frac{1}{2}k\ x^2=\ \frac{1}{2}\ m\ v^2$$

$$k\ x^2=\ m\ v^2$$

$$v^2=\ \frac{k\ x^2}{m}$$

$$v=\ \sqrt{\frac{k\ x^2}{m}}$$

$$v=\ x\ \sqrt{\frac{k}{m}}$$

$$v=\ 0,072\ m\ \sqrt{\frac{1500\ N/m}{0,08\ g}}$$

$$v=9,9\ m/s$$

6. Fuentes

Traful, UTEM. (2016). Aplicación de la conservación de la energía mecánica. Recuperado de: https://www.youtube.com/watch?v=5Ylxn5VWm-A

Traful, UTEM. (2016). Energía potencial y conservación de la energía. Recuperado de: https://www.youtube.com/watch?v=jG0zDp3rZVk

Traful, UTEM. (2016). Trabajo y energía cinética. Recuperado de: https://www.youtube.com/watch?v=KtSjhb3EMx4

Traful, UTEM. (2016). Trabajo mecánico y potencia. Recuperado de: https://www.youtube.com/watch?v=MZdNjS5_60I

University of Colorado. (s.f.). Energía en la pista de patinaje [simulación interactiva]. Recuperado de: https://phet.colorado.edu/sims/html/energy-skate-park-basics/latest/energy-skate-park-basics_es.html