1. Sumario

• Mediciones y las unidades
• El Sistema Internacional
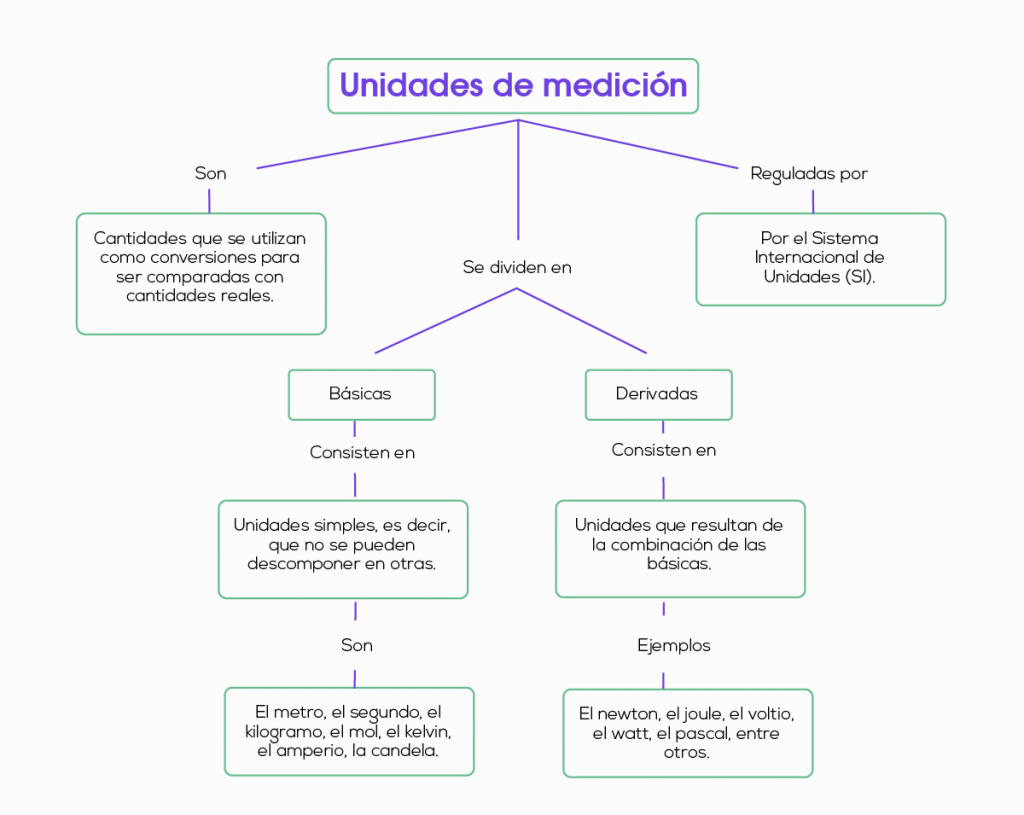
• Unidades básicas y unidades derivadas
• Conversiones de unidades
• Cantidades vectoriales y cantidades escalares
• Vectores
• Operaciones vectoriales

2. Objetivo

Al finalizar el estudio de este capítulo, entre otras habilidades, usted será capaz de:

• Reconocer la Física como ciencia y las principales herramientas que utiliza, para la comprensión de su funcionamiento en la descripción del universo.

3. Introducción

A continuación, se presentan una serie de sugerencias para cumplir con las experiencias de aprendizaje, que se proponen en el programa del curso de de Física I (teoría). Si bien son aplicables al curso, no son exhaustivas, por lo cual, el estudiante puede aprovechar otros materiales recomendados en las referencias bibliográficas.

4. Guía de lectura y recursos adicionales

1. Debe efectuar la lectura de las secciones del libro en las cuales se trabajen los temas contenidos en el sumario. Preste particular atención a los conceptos de factor de conversión, escalares y vectores, componentes y dirección de un vector, resultante. Puede elaborar materiales de estudio como los comentados en la sección “Consideraciones metodológicas”. Además de la lectura, se le sugiere a continuación una serie de recursos de apoyo para su estudio.
2. Video sobre el concepto de medición. Enlace: https://www.youtube.com/watch?v=tn_1LR0e_Ps (Duración: 25 minutos)
3.  Video sobre el Sistema Internacional. Enlace: https://www.youtube.com/watch?v=pyZi1H0B4jQ (Duración: 24 minutos)
4. Material escrito sobre unidades, prefijos y conversiones. Enlace: https://www.frro.utn.edu.ar/repositorio/secretarias/sac/ingreso/archivos/Unidad_1_fisica.pdf (Extensión: 14 páginas)
5. Espacio de experimentación con vectores (simulación). Enlace: https://phet.colorado.edu/es/simulation/vector-addition

5. Esquemas y ejemplos

Mapa conceptual

A continuación, se le muestra un ejemplo de mapa conceptual sobre unidades de medición.

Cuadro sinóptico

A continuación, se le muestra un ejemplo de cuadro sinóptico sobre las operaciones vectoriales

Operación		Procedimiento
Multiplicación de un escalar por un vector	$$c\bullet\vec{A}$$	Se multiplica la magnitud del vector por el escalar. La dirección no cambia.	$$\vec{c\bullet A}$$
Suma de vectores	$$\vec{A}+\vec{B}$$	Se suman las componentes horizontales de un vector con las del otro y, por aparte, se hace lo mismo con las componentes verticales. Luego, se obtiene la magnitud y dirección a partir de dichas componentes	$$R_x=\ A_x+B_x $$ $$R_y=\ A_y+B_y$$ $$\left|\vec{R}\right|=\ \sqrt{{R_x}^2+{R_y}^2}$$ $$\theta=\ \tan^{-1}{\left(\frac{R_y}{R_x}\right)} $$
Resta de vectores	$$\vec{A}-\vec{B}$$	Se suma la componente horizontal del primer vector con el negativo de la horizontal del otro y, por aparte, se hace lo mismo con las componentes verticales. Luego, se obtiene la magnitud y dirección a partir de dichas componentes.	$$R_x=\ A_x+\left(-B_x\right)$$ $$R_y=\ A_y+\left(-B_y\right)$$ $$\left|\vec{R}\right|=\ \sqrt{{R_x}^2+{R_y}^2}$$ $$\theta=\ \tan^{-1}{\left(\frac{R_y}{R_x}\right)}$$

Ejercicios resueltos

A continuación, se presentan dos ejercicios resueltos, uno sobre el tema de conversiones de unidades y otro sobre operaciones con vectores.

Ejercicio No. 1.  La aceleración de la gravedad en nuestro planeta es de 115 200 pies sobre minutos al cuadrado. Calcule a cuánto equivale dicha aceleración, pero empleando unidades del SI.

$$115200\ \frac{ft}{{min}^2}\ x\ \frac{0,3048\ m}{1\ ft}\ x\ \frac{\left(1\ min\right)^2}{\left(60\ s\right)^2}=9,75\ m/s^2$$

Ejercicio No. 2.  Considere los siguientes vectores:

Determine la magnitud y dirección de $\vec{V}-\ \vec{J}$

$$V_x=-\ 4,1\ N\ast cos70°= -1,40 N$$

$$V_y=-\ 4,1\ N\ast sen70°= -3,85 N$$

$$J_x=2,5\ N\ast cos40°= 1,92 N$$

$$J_y=2,5\ N\ast sen40°= 1,61 N$$

$$R_x=-\ 1,40\ N-1,92\ N=\ -3,32\ N$$

$$R_y=-\ 3,85\ N-\ 1,61\ N=\ -5,46\ N$$

$$R=\ \sqrt{{(-3,32\ N)}^2+{(-5,46\ N)}^2}$$

$$\fbox{$R=6,39\ N$}$$

$$\theta=\ \tan^{-1}{\left(\frac{R_y}{R_x}\right)}+180°$$

$$\theta=\ tan^{-1}{\left(\frac{-5,46 N}{-3,32 N}\right)}+180°$$

$$\fbox{$\theta=\ 238,7°$}$$

Más ejercicios

Para más ejercicios resueltos, puede consultar el canal en YouTube de la ECEN. Enlace: https://www.youtube.com/channel/UCZWdZ78Ue9fZroLOCrSGz5A/videos

6. Fuentes

Canal Encuentro. (2017). En su justa medida: ¿Qué es medir? Recuperado de: https://www.youtube.com/watch?v=tn_1LR0e_Ps

Canal Encuentro. (2017). En su justa medida: Sistema Internacional de Unidades. Recuperado de: https://www.youtube.com/watch?v=pyZi1H0B4jQ

Prodanoff, F. (s.f). Física. Unidad 1: Magnitudes y unidades de medida. Recuperado de: https://www.frro.utn.edu.ar/repositorio/secretarias/sac/ingreso/archivos/Unidad_1_fisica.pdf

University of Colorado. (s.f.). Adición de vectores [simulación interactiva]. Recuperado de: https://phet.colorado.edu/es/simulation/vector-addition

Vargas, I. (2002). Vectores: teoría y práctica. Espacio virtual de la física, 2 (1), pp. 1-35.